Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 09. 08. 2013 16:33
- grizzlybear

- Příspěvky: 27
- Škola: MFF UK
- Pozice: student
- Reputace: 1
dva druhy nekonečna
Problém nemám nějak jasně definovaný a nejsem si správně jist kategorií...
Matně si pamatuju, že jedno nekonečno souvisí s mohutností přirozených čísel, říkejme mu nekonečno-a. A druhé nekonečno souvisí s mohutností reálných čísel- říkejme nekonečno-b. Prakticky jsem ale vždycky počítal jen s jedním nekonečnem značeným ležatou osmičkou- nevím, které z těch dvou to pak bylo. Tipoval bych, že třeba v sumě, co jde do nekonečna jde o nekonečno-a...
Jsou nějaká pravidla pro počítání s nekonečny?
opět, čekám že: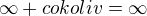
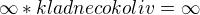
až na neurčité výrazy:
lze ale říct např, že:
a podobně? Pracujete někdy s dvěma nekonečny nebo jen s jedním?
Offline
#2 09. 08. 2013 17:15 — Editoval Brano (09. 08. 2013 17:32)
Re: dva druhy nekonečna
Nechcem ta velmi popliest, ale prisne vzate je ta lezata osmicka uplne iny typ nekonecna ako kardinalne cisla. Ak uz by si chcel symbol  z analyzy zlucit s nejakym kardinalnym cislom, tak je asi najrozumnejsie ho zlucit s
z analyzy zlucit s nejakym kardinalnym cislom, tak je asi najrozumnejsie ho zlucit s  , co je kardinalita (=mohutnost) prirodzenych cisel. Kardinalita realnych cisel je
, co je kardinalita (=mohutnost) prirodzenych cisel. Kardinalita realnych cisel je  . Inak kardinalnych cisel je strasne vela. Malicko z nich je konecnych - to su prirodzene cisla. Ostatne su nekonecne a ich pocet je taky, ze sa ani "nezmestia" do ziadnej mnoziny.
. Inak kardinalnych cisel je strasne vela. Malicko z nich je konecnych - to su prirodzene cisla. Ostatne su nekonecne a ich pocet je taky, ze sa ani "nezmestia" do ziadnej mnoziny.
Potom co sa tyka odcitavania kardinalnych cisel, tak to sa obvykle nedefinuje, lebo ho nie je treba, ale keby si velmi chcel, tak kedze pre nekonecne 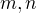 plati, ze ak
plati, ze ak  potom
potom 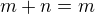 mozes pre
mozes pre  definovat
definovat  .
.
V analyze sa tiez pracuje s viac nekonecnamy, ale lisia sa inym sposobom ako velkostou. V kontexte realnych cisel su dve 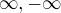 take, ze
take, ze  tvori dvojbodovu kompaktifikaciu
tvori dvojbodovu kompaktifikaciu  homeomorfnu s uzavretym intervalom, zatial co
homeomorfnu s uzavretym intervalom, zatial co  v komplexnych cislach je take, ze
v komplexnych cislach je take, ze 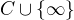 je jednobodova kompaktifikacia
je jednobodova kompaktifikacia  homeomorfna so sferou.
homeomorfna so sferou.
Offline
#3 09. 08. 2013 17:51
- grizzlybear

- Příspěvky: 27
- Škola: MFF UK
- Pozice: student
- Reputace: 1
Re: dva druhy nekonečna
↑ Brano:
dík, zajímavý. Vyznívá to tak, že kardinalita se řeší v matematice, kterou mi nevykládali. :) S tím sčítáním se mi to líbí, i když to neumím dokázat. :)
Jinak nerozumím:
"Kardinalita realnych cisel je  . Inak kardinalnych cisel je strasne vela. Malicko z nich je konecnych - to su prirodzene cisla. Ostatne su nekonecne a ich pocet je taky, ze sa ani "nezmestia" do ziadnej mnoziny."
. Inak kardinalnych cisel je strasne vela. Malicko z nich je konecnych - to su prirodzene cisla. Ostatne su nekonecne a ich pocet je taky, ze sa ani "nezmestia" do ziadnej mnoziny."
Ale asi to nech být, lehce jsem koukal na:
http://en.wikipedia.org/wiki/Cardinal_number
Asi se na pojem nekonečna dívám nepříliš abstraktně: "nekonečně dlouhý provázek". A reálná čísla :-/ "...nekonečná hustota v jednom bodě". Jak vidmo s takovýma představama se daleko nedojde. Ostatně i k pojmu číslo přistupuju intuitivně, teorii množin neznám.
Ale ještě teda v té analýze. Když sčítám nekonečnou řadu, tak si říkám, že to je řada o velikosti přirozených čísel- asi nejde sčítat řadu co má mohutnost reálných čísel...
A pak mi vyjde, že řada diverguje (nebo integrál) a vyjde  to je taky nekonečno_a neboli
to je taky nekonečno_a neboli  ?
?
Ještě mě napadá: nehraje tohle roli v teorii míry- pro funkci co je 0 na racionálních číslech a 1 na reálných (bez racionálních) na intervalu např. (0,1) vyjde integrál jedna? Nebo to je s dvěma druhy nekonečna zcela nesouvisející otázka?
Offline
#4 09. 08. 2013 17:57
- grizzlybear

- Příspěvky: 27
- Škola: MFF UK
- Pozice: student
- Reputace: 1
Re: dva druhy nekonečna
↑ Brano:
jo, něco s tou sférou se mi vybavuje. Chápu, že v matematice jde o přesné a abstraktní vyjádření, ale prakticky spíš pracuju s vlastní představou... Dvě nekonečna v R jsou představou nekonečného špagátu. V C se představujou hůř- tam bych řek, že jsou nekonečna "na všechny strany", což bude právě ten pól sféry- nejspíš.
Offline
#5 09. 08. 2013 18:23 — Editoval Brano (09. 08. 2013 18:27)
Re: dva druhy nekonečna
1) Kardinalne cisla sa ucia v teorii mnozin a aspon trosku ste z nej mali, kedze si polozil povodnu otazku.
2) v ramci teorie mnozin sa da ukazat, ze neexistuje "mnozina vsetkych kardinalnych cisel" co je ekvivalentne tomu, ze neexistuje mnozina vsetkych mnozin. To suvisi s Russelovym paradoxom.
3) Da sa v istom zmysle scitat aj nespocitatelne vela cisel (mozem napisat v akom, ak chces), ale ak to ma konvergovat (v tom zmysle co mam na mysli :-)) tak tych cisel moze byt najviac spocitatelne vela nenulovych (to tam vyjde ako veta)
4) To s tym integralom je tak ako pises (ak je to teda Lebesgueov integral) a vyznamnu rolu hra presne to, ze ta fcia je  okrem zopar vynimiek, ktorych je iba spocitatelne vela (
okrem zopar vynimiek, ktorych je iba spocitatelne vela (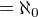 ) - tu sa jedna o pocet zlych bodov a pocet je kardinalne cislo.
) - tu sa jedna o pocet zlych bodov a pocet je kardinalne cislo.
5) V  je obvykle iba to jedno nekonecno - co moze byt napr. severny pol tej sfery a kazdym smerom sa dostanes do toho isteho nekonecna. To neznamena, ze by sa nedali vymysliet nekonecna pre kazdy smer, ale nerobi sa to. Rychlo by si prisiel na to, ze keby si isiel "do nekonecna" po nejakej spirale, tak sa nedostanes ani do jedneho z nich a skoncil by si pri tom, ze by si definoval nekonecno pre kazdu neohranicenu krivku (a tam hladal nejake triedy ekvivalencii) a to by bola asi uz fakt moc neprehladne.
je obvykle iba to jedno nekonecno - co moze byt napr. severny pol tej sfery a kazdym smerom sa dostanes do toho isteho nekonecna. To neznamena, ze by sa nedali vymysliet nekonecna pre kazdy smer, ale nerobi sa to. Rychlo by si prisiel na to, ze keby si isiel "do nekonecna" po nejakej spirale, tak sa nedostanes ani do jedneho z nich a skoncil by si pri tom, ze by si definoval nekonecno pre kazdu neohranicenu krivku (a tam hladal nejake triedy ekvivalencii) a to by bola asi uz fakt moc neprehladne.
Offline
#6 09. 08. 2013 18:35
- grizzlybear

- Příspěvky: 27
- Škola: MFF UK
- Pozice: student
- Reputace: 1
Re: dva druhy nekonečna
↑ Brano:
Díky, já bych to nechal být. Ta 3) mě docela zaujala.
Offline
#8 09. 08. 2013 20:39
Re: dva druhy nekonečna
Ak chceme vnimat integral ako sucet cez nespocitatelnu mnozinu, co je rozumna predstava, tak este treba poznamenat, ze v skutocnosti scitavame nekonecne male cisla. Totizto ak integrujeme napr.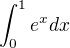 tak nescitavame
tak nescitavame  pre
pre ![kopírovat do textarea $x\in[0,1]$](/mathtex/a3/a35805693e94e4f44290ccd56f46ee4a.gif) ale
ale 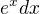 kde to
kde to 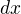 je cosi nekonecne male.
je cosi nekonecne male.
Idea suctu cisel (t.j. nie nekonecne malych veciciek) cez akokolvek velku indexovu mnozinu sa da zachytit takto:
Uvazujme  pricom vsetky
pricom vsetky 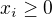 a
a  je lubovolna neprazdna indexova mnozina.
je lubovolna neprazdna indexova mnozina.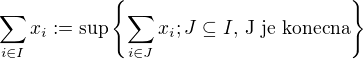
t.j. urobime vsetky mozne konecne sucty co sa daju a vezmeme ich supremum. So zapornymi cislami sa vysporiadame obvyklym sposobom, sucet kladnej casti, sucet zapornej casti a potom ich odratame, ak je ten rozdiel dobre definovany.
Offline
#9 12. 08. 2013 10:34 — Editoval Rumburak (12. 08. 2013 11:28)
Re: dva druhy nekonečna
↑ grizzlybear:
Ahoj. To nekonečno vyjádřené ležatou osmičkou odpovédá představě "nekonečně vzdáleného bodu" -
jak jsi správně napsal, jde o abstrakci.
Na reálné ose uvažujeme takové "body" dva, jeden "napravo od nuly" , druhý "nalevo od nuly".
V komplexní rovině by takových nevlastních bodů mohlo být nekonečně mnoho (například na každou hlavní hodnotu argumentu
by analogicky jako u polopřímky mohl připadnout jeden), ale ukazuje se jako výhodnější zavést zde pouze jeden nevlastní bod
společný pro všechny polopřímky - pomocí stereografické projekce na sféru.
Najdu-li pěkný odkaz, dám ho sem.
EDIT. Pro představu by měl postačit druhý obrázek zde .
Offline
#10 12. 08. 2013 10:54 — Editoval jarrro (12. 08. 2013 10:54)
Re: dva druhy nekonečna
↑ Rumburak:ahoj viem, že je to trochu OT, ale platí v komplexnej analýze
kde
a nekonečno na konci je komplexné nekonečno ?
MATH IS THE BEST!!!
Offline
#11 12. 08. 2013 11:22 — Editoval Rumburak (12. 08. 2013 11:23)
Re: dva druhy nekonečna
↑ jarrro:
Ahoj.
Pokud ještě přidáme předpoklady  a
a 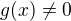 na některém redukovaném okolí bodu
na některém redukovaném okolí bodu 
( může být i
může být i  ) , pak ano.
) , pak ano.
Plyne to z faktu, že na tzv. uzavřené Gaussově rovině  zavádíme topologii tak, aby
zavádíme topologii tak, aby
stereografická projekce byla homeomorfismem (tedy spojitá "tam i zpět") , díky čemuž za fundamentální systém
okolí bodu  v
v  můžeme považovat množinové doplňky uz. kruhů se středem v bodě 0.
můžeme považovat množinové doplňky uz. kruhů se středem v bodě 0.
Nejsem si jist, zda jsem neudělal někde chybu v terminologii, od školy mám už určitý časový odstup . :-)
Offline
#12 12. 08. 2013 11:31 — Editoval jarrro (12. 08. 2013 11:35)
Re: dva druhy nekonečna
↑ Rumburak:díky c rôzne od nuly som zabudol napísať a g rôzne od nuly to plynie zo toho, že sa pýtame na limitu podielu keby bolo na ľubovoľne malom redukovanom (to znamená, že je z neho vylúčený bod alfa?) okolí alfa g niekde nulové potom by tá limita nemohla z princípu existovať, lebo by neexistovala ani funkcia (podiel) na okolí alfa a otázka nemala zmysel je to tak?
MATH IS THE BEST!!!
Offline
#13 12. 08. 2013 12:02
Re: dva druhy nekonečna
Poznamka:
V urcitom zmysle tu
http://en.wikipedia.org/wiki/Non-standard_analysis
sa najde odpoved na polozenu otazku na zaciatku.
Pekna teoria v ktorej su casto jednoduchsie dokazy ako obycajne.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#14 12. 08. 2013 12:07
Re: dva druhy nekonečna
↑ vanok:
Nestandardna analyza pracuje s nekonecne velkymi cislami (potom aj nekonecne malymi) ktore su este uplne ine ako tie na ktore sa pytal, ale ak sa nemylim, tak  sa tu da chapat ako nejaka trieda ekvivalencie, ktora obsahuje vsetky nekonecne velke cisla. Je to tak?
sa tu da chapat ako nejaka trieda ekvivalencie, ktora obsahuje vsetky nekonecne velke cisla. Je to tak?
Offline
#15 12. 08. 2013 12:26
Re: dva druhy nekonečna
Ahoj ↑ Brano:,
Tu je jedna pristupna kniha
http://www.math.wisc.edu/~keisler/calc.html
O limitach sa pisé v kapitole 5.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#16 12. 08. 2013 16:58
Re: dva druhy nekonečna
g rôzne od nuly to plynie zo toho, že sa pýtame na limitu podielu keby bolo na ľubovoľne malom redukovanom (to znamená, že je z neho vylúčený bod alfa?) okolí alfa g niekde nulové potom by tá limita nemohla z princípu existovať, lebo by neexistovala ani funkcia (podiel) na okolí alfa a otázka nemala zmysel je to tak?
I když si nejsem úplně jist, zda jsem tento poměrně složitě zformulovaný dotaz pochopil zcela správně, připadá mí, že to odpovídá tomu,
co jsem myslel. (Redukované okolí stejně jako prstencové okolí v české terminologii skutečně znamená okolí, z něhož je vyňat jeho střed,
což pro definici limity potřebujeme) .
Mezitím mne napadlo násleující.
V komplexní analýze se někdy definuje  (analogicky.
(analogicky.  ) .
) .
Při této konvenci by předpoklad o nenulovém jmenovateli byl v té větě zbytečný.
Offline
#17 12. 08. 2013 20:21
Re: dva druhy nekonečna
↑ Rumburak:díky myslel som to tak, že ak má byť ten podiel komplexné číslo tak g nemôže byť nulové a ak má existovať limita nejakej funkcie tak musí v prvom rade byť definovaná na nejakom redukovanom okolí v príslušnom bode . z toho dôvodu som predpoklad o nenulovosti g nepísal
MATH IS THE BEST!!!
Offline
#18 13. 08. 2013 10:03 — Editoval Rumburak (13. 08. 2013 10:10) Příspěvek uživatele Rumburak byl skryt uživatelem Rumburak. Důvod: Odesláno omylem.
#19 13. 08. 2013 10:56
Re: dva druhy nekonečna
↑ jarrro:
Ahoj. Omluv mne, pokud jsem po ránu ještě trochu rozespalý a pomalejší v chápání. :-) . Nicméně smysl tohoto Tvého sdělení
myslel som to tak, že ak má byť ten podiel komplexné číslo tak g nemôže byť nulové a ak má existovať limita nejakej funkcie tak musí v prvom rade byť definovaná na nejakom redukovanom okolí v príslušnom bode . z toho dôvodu som predpoklad o nenulovosti g nepísal
chápu tak, že onen předpoklad o nenulovosti funkce  na nějakém redukovaném okolí bodu
na nějakém redukovaném okolí bodu  jsi pojal - dalo by se říci - implicitně.
jsi pojal - dalo by se říci - implicitně.
Ale k tomu jsi použil de facto předpoklad, že existuje limita toho podílu - ze samotných předpokladů
(1) 
to nevyplývá. Avšak z (1) nevyplývá ani existence limity onoho podílu - pokud nemáme přijatu definici  , o níž jsem se zmínil minule,
, o níž jsem se zmínil minule,
a která situaci okolo přirozených definičních oborů mnohých funkcí významně mění .
O.K. ?
Offline
#20 13. 08. 2013 11:40
Re: dva druhy nekonečna
↑ Rumburak:ahoj vidíš to ma nenapadlo, ale z existencie podielu na redukovanom okolí alfa vyplýva existencia limity (za daných predpokladov o f g) nie?
či môžu existovať také f g tak, že podiel na nejakom okolí alfa (redukovanom) existuje, ale jeho limita neexistuje? predpoklady o f g sú
MATH IS THE BEST!!!
Offline
#21 13. 08. 2013 17:00 — Editoval Rumburak (13. 08. 2013 17:10)
Re: dva druhy nekonečna
↑ jarrro:
Správná je ta první varianta. Když na některém redukovaném okolí  bodu
bodu  bude
bude 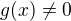 , pak tam budou mít smysl podíly
, pak tam budou mít smysl podíly  . Z předpokladu
. Z předpokladu 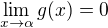 snadno plyne
snadno plyne 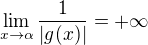 (limita reálné funkce
(limita reálné funkce
komplexní proměnné). Z předpokladu  vyplývá existence konstanty
vyplývá existence konstanty  a redukovaného
a redukovaného
okolí  bodu
bodu  , na němž je
, na němž je  . Takže na této množině
. Takže na této množině  , která je redukovaným okolím bodu
, která je redukovaným okolím bodu  , platí
, platí
(1)  .
.
Pro 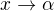 jde
jde 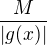 k
k  , takže tamtéž musí podle (1) jít i
, takže tamtéž musí podle (1) jít i 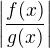 (opět jde o limity reálných funkcí kompl. prom.). Odtud
(opět jde o limity reálných funkcí kompl. prom.). Odtud
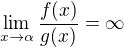 -
-
************
Důkaz pro situaci, kdy nenulové k.č. je dovoleno dělit nulou s výsledkem  , jistě netřeba blíže rozebírat.
, jistě netřeba blíže rozebírat.
Offline
#22 13. 08. 2013 20:26
Offline