Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 16. 08. 2013 15:37 — Editoval Mirgeee (16. 08. 2013 15:47)
Re: Trigonometrická identita
Na intervalu -pi/2 až pi/2 se f(x) = x. Pokud bych chtěl definovat f(x) pro všechna R, tak bych musel chování této funkce nejspíš nějak rozdělit podle hodnoty x, ne?
Třeba kdyby bylo x v intervalu -pi/2 + 2kpi až pi/2 + 2kpi, pak by se f(x) = x - 2kpi pro k celé.
A něco podobného udělat pro druhý a třetí kvadrant:
f(x) = pi - (x - 2kpi) pro x z pi/2 + 2kpi až pi + 2kpi
f(x) = pi + (x - 2kpi) pro x z -pi + 2kpi až - pi/2 + 2kpi
Jak ale dokázat tu rovnost? Asi je třeba nějak dokázat, že všem x z jednotlivých intervalů přiřadí odpovídající f(x)...
Offline
#3 16. 08. 2013 16:00 Příspěvek uživatele Rumburak byl skryt uživatelem Rumburak. Důvod: chybná úvaha
#4 16. 08. 2013 19:17
- Eratosthenes
- Příspěvky: 2937
- Reputace: 139
Re: Trigonometrická identita
↑ Mirgeee:
Ahoj,
definičním oborem funkce 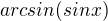 je množina všech reálných čísel. Vezmi si libovolné reálné číslo. Funkce sinus z něj "vyrobí" číslo z intervalu
je množina všech reálných čísel. Vezmi si libovolné reálné číslo. Funkce sinus z něj "vyrobí" číslo z intervalu  a to je právě definiční obor funkce arcsin.
a to je právě definiční obor funkce arcsin.
Budoucnost patří aluminiu.
Offline
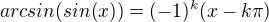 ,
,![kopírovat do textarea $k = [{{x+\pi/2}\over \pi}]$](/mathtex/b8/b86a1c5fe00ad0d0088e69dc5fff4f95.gif)