Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 17. 08. 2013 18:04 — Editoval marnes (17. 08. 2013 18:05)
- marnes

- Příspěvky: 11227
Re: stred kružnice
↑ Tamara11:
Možností je více.
Osobně bych použil průsečík dvou os stran ( při předpokladu kružnice opsané)
Jo. A na začátku vás zdravím.
Offline
#3 17. 08. 2013 18:05 Příspěvek uživatele bonifax byl skryt uživatelem bonifax. Důvod: o minutu později :X :D
#4 18. 08. 2013 15:24
- grizzlybear

- Příspěvky: 27
- Škola: MFF UK
- Pozice: student
- Reputace: 1
Re: stred kružnice
Mě napadlo vzít si rovnici kružnice a do ní dosadit body a pak to nějak upočítat.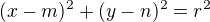 m, n je střed kružníce.
m, n je střed kružníce.
takže:

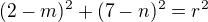
myslím, že to vede na lineární rovnici.
Offline
#5 18. 08. 2013 20:40
#6 18. 08. 2013 21:12 — Editoval Brano (18. 08. 2013 21:16)
Re: stred kružnice
↑ grizzlybear: Cim dostaneme tri kvadraticke rovnice o troch neznamych, co by mohlo stredoskolaka zastrasit. Na druhu stranu vyriesia sa pomerne lahko - mozeme odpocitat tretiu rovnicu (prisluchajucu  ) od prvej aj druhej a dostaneme dve linearne rovnice (ako si spravne poznamenal) o dvoch neznamych
) od prvej aj druhej a dostaneme dve linearne rovnice (ako si spravne poznamenal) o dvoch neznamych 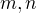 , ktore, nie velmi prekvapivo, zodpovedaju osiam useciek
, ktore, nie velmi prekvapivo, zodpovedaju osiam useciek  a
a 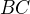 ; ako navrhoval ↑ marnes:
; ako navrhoval ↑ marnes:
Offline
#7 19. 08. 2013 07:58 — Editoval Cheop (19. 08. 2013 08:20)
- Cheop


- Místo: okres Svitavy
- Příspěvky: 8209
- Škola: PEF VŠZ Brno (1979)
- Pozice: důchodce
- Reputace: 366
Re: stred kružnice
↑ Tamara11:
No a já bych využil to, že: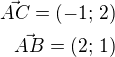
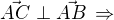
střed kružnice je uprostřed strany BC tedy: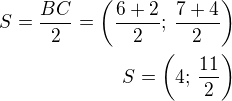
Nikdo není dokonalý
Offline

 ? dakujem
? dakujem