Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 27. 08. 2013 12:51
Dvě padající koule
Dva míčky o hmotnostech 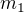 a
a 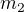 , kde
, kde  umístěné nad sebou tak, že
umístěné nad sebou tak, že
lehčí je nad těžším, pustíme na zem z výšky  . Vypočítejte výšky
. Vypočítejte výšky 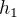 a
a 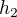 , do
, do
kterých míčky po odrazu od země vyskočí. Pro jaký poměr hmotností vyskočí
lehčí míček nejvýše a jaká je tato výška? Předpokládejte přitom, že všechny
rázy jsou dokonale pružné, že rozměry míčků můžeme oproti výškám h, 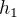 a
a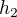 zanedbat a že jejich pohyb před a po odrazu probíhá podél přímky.
zanedbat a že jejich pohyb před a po odrazu probíhá podél přímky.
Nemám problém s tím, si situaci nějak představit. Mám problém s výpočtem. V nějakém bodě dělám chybu a nevím kde. Nikdy se nedostanu ke správné odpovědi. Chci poprosit, jestli by tu někdo nemohl rozepsat řešení. Zatím aspoň jak se dostat k výškám 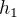 ,
, 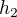 . Ze všech různých kombinací rovnic s kinetickou energií a hybností se mi nedaří vyjádřit jednu nezávisle na druhé.
. Ze všech různých kombinací rovnic s kinetickou energií a hybností se mi nedaří vyjádřit jednu nezávisle na druhé.
Offline
#2 27. 08. 2013 17:15
- grizzlybear

- Příspěvky: 27
- Škola: MFF UK
- Pozice: student
- Reputace: 1
Re: Dvě padající koule
Hodilo by se napsat, co vlastně víš. Nemusel bych se pak tolik namáhat v uvažování.
Nicméně, jak jsem si to představil (neříkám, že to je správně). Ten těžší míček se odrazí dřív než ten lehčí a půjde stejnou rychlostí proti němu. (tohle je předpoklad, nevím jak si jinak poradit s tím, že oba dopadnou "naráz"). V rovnicích se to projeví spíš zjednodušením situace, i když ani tak to nebude snadné.
Energie (před srážkou= po srážce)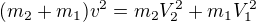
Hybnost (před srážkou= po srážce)
- tady může vzniknout chyba ve znaménku. Musíme uvažovat vektorově, tj. jakým směrem to působí. Já považuju směr nahoru za kladný (co míří nahoru je s plusem). 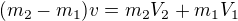
Teď je třeba si v tom zmatku uvědomit, co je neznámá. Jsou to ty s velkými písmeny- tj. rychlosti. Rychlost v vlevo od rovnítka jde určit z potenciální energie.  .. To co je teď složité a do čeho se mi nechce je vyjádření jedné z rychlostí. Je nejspíš jedno kterou. A je asi rozumější spíš z rovnice hybnosti . Tj.
.. To co je teď složité a do čeho se mi nechce je vyjádření jedné z rychlostí. Je nejspíš jedno kterou. A je asi rozumější spíš z rovnice hybnosti . Tj.  . To umocníš na druhou a dosadíš do energie. Tím ti vyjde v nejhorším kvadratická rovnice. Ale možná ne :) a bude lineární. Protože by ti mělo vyjít jednoznačné řešení. (kvadratická by mohla mít dvě).
. To umocníš na druhou a dosadíš do energie. Tím ti vyjde v nejhorším kvadratická rovnice. Ale možná ne :) a bude lineární. Protože by ti mělo vyjít jednoznačné řešení. (kvadratická by mohla mít dvě).
Je možný, že existuje snazší řešení. Já ho ale nevidím.
Offline
#3 27. 08. 2013 17:33
Re: Dvě padající koule
↑ grizzlybear: no ale potřebuji 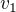 a
a 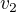 nezávisle na sobě. To je právě to. Dostanu rovnici kin. energie a hybnosti a z nich se má dojít k vyjádření rychlostí nezávisle na sobě, ale mně to nikdy nevyjde. Potřebuji vědět postup, jakým tu soustavu rovnic řešit. Když si vyjádřím
nezávisle na sobě. To je právě to. Dostanu rovnici kin. energie a hybnosti a z nich se má dojít k vyjádření rychlostí nezávisle na sobě, ale mně to nikdy nevyjde. Potřebuji vědět postup, jakým tu soustavu rovnic řešit. Když si vyjádřím 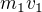 z rovnice hybností a dosadím do rovnice kin. energie, vyjde mi, že
z rovnice hybností a dosadím do rovnice kin. energie, vyjde mi, že 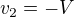 , což je úplně špatně.
, což je úplně špatně.
Offline
#4 27. 08. 2013 20:00
Re: Dvě padající koule
↑ Annmn:
Vyjdeme z rovnic od ↑ grizzlybear:, jen si hledané rychlosti označím  a
a 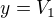 , abych se nemusel babrat s indexy
, abych se nemusel babrat s indexy
malý trik: protože hledáme poměr hmotností, tak si ho přímo zavedeme jako parametr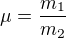 podle podmínek zadání je
podle podmínek zadání je 
Nyní obě rovnice vydělíme 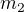 a dostaneme
a dostaneme
Z druhé rovnice je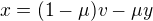 a dosadíme do první
a dosadíme do první![kopírovat do textarea $(1+\mu )v^2=[(1-\mu)v-\mu y]^2+\mu y^2$](/mathtex/fa/fa1db3dd472ba8c8f7e90eafff0e37bf.gif)
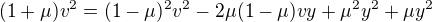
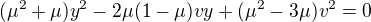
Tohle je normální kvadratická rovnice pro  , kterou vyřešíme
, kterou vyřešíme
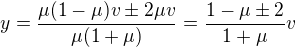
Protože chceme, aby rychlost byla kladná (to je směr nahoru), bude vyhovovat jen řešení s 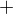


Pořádek je pro blbce, inteligent zvládá chaos!
Offline
#5 27. 08. 2013 23:43
- grizzlybear

- Příspěvky: 27
- Škola: MFF UK
- Pozice: student
- Reputace: 1
Re: Dvě padající koule
Plet jsem se v tom, že kvadratická rovnice dává principiálně špatný výsledek. Ten výsledek, co jsme zavrhli: "záporná rychlost" Je vlastně rychlost před srážkou. y=-v (první těleso padá dolů rychlostí v). Ke všemu překvapení rychlost x=v tj. těleso letí nahoru. Tobě se nějakým způsobem podařilo dojít k řešení, i když neužitečnému.
Nicméně i tak mám pocit, že je někde chyba- ve výrazu pro y těžko najdeme extrém. Mě na první pohled přijde, že maximum je pro mí=0, což je nefyzikální y=3v. Druhý kraj je mí=1 y=2/2v=v. Funkce je pro mu klesající, tj. nemá extrém.
Pokud jsme neudělali chybu (a nejspíš ne), máme to správně spočítáno, ale odpověď není konkrétní- tj. čím lehčí m1, tím větší získá rychlost a tím výš vyskočí. (s hrůzou dalšího počítání dodávám: po prvním odrazu- úloze by odpovídalo, že se můžou odrazit víckrát).
Ale stejně ještě nevím, jestli ta moje počáteční rychlost v- je správně (obecně by mohli být jakékoliv, aby kynetická energie míčků dávala potenciální energii na začátku). K snazšímu vyřešení by se hodilo znát výsledek. :)
Nevím, jestli ti moje řeči pomohly, ale to zdenkovo mi přijde pochopitelný, byť nevím, jestli je správný ten můj začátek.
Offline
#6 28. 08. 2013 09:21
Re: Dvě padající koule
grizzlybear napsal(a):
K snazšímu vyřešení by se hodilo znát výsledek. :)
Viz http://fyzika.feld.cvut.cz/~cervenka/vy … iklady.pdf
Příklad 5.3 - výsledky na konci materiálu
Pokud se tedy nemýlím.
Offline