Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#5 05. 09. 2013 15:08
Re: konvergence řady
↑ Stýv:
tak ja znam jen to leibnitzovo kriterium, ze pokud dokazu absolutni konvergenci te rady, tak pak je ta rada konvergentni. Jeste jsem ted nasla na netu ze pokud dokazu ze ten vyraz bez (-1)^n je nerostouci posl a lim toho je 0, pak je rada konvergetni, tohle si myslel?
Offline
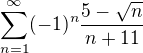

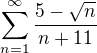 konverguje, na tom se prave zaseknu:(
konverguje, na tom se prave zaseknu:(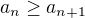 ale to se teda zasekavam v prvnim kroku
ale to se teda zasekavam v prvnim kroku 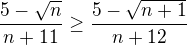 a dal nevim jak to mam upravit:(
a dal nevim jak to mam upravit:( jde k nule
jde k nule