Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 19. 09. 2013 21:33
kinematika 2
Děkuji za vysvětlení příkladu 1 :), teď jsem narazila na další, který je určitě lehký, ale já tomu prostě nemůžu přijít na kloub:
Veslice plující po řece urazila vzdálenost 120 m při plavbě po proudu za 12 s, při plavbě proti proudu za 24 s. Určete velikost rychlosti veslice vzhledem k vodě a velikost rychlosti proudu v řece. Obě rychlostí jsou stálé.
Výsledek je 7,5 a 2,5 m/s.
Děkuji moc.
Offline
#2 19. 09. 2013 21:45
Re: kinematika 2
Ahoj,
první příklad jsem ti sice vysvětlil, ale u tohohle už se možná trošku zastavíme. Co přesně ti dělá problém? Nevíš vůbec, jak do toho jít, nebo víš, ale něco ti nevychází?
Jimmy
Což je to možné! Tento stařičký světec ještě ani nezaslechl v svém lese, že bůh je mrtev!
Offline
#4 19. 09. 2013 22:22
Re: kinematika 2
↑ Bak:
Voda tu loď nese. I když nebudu veslovat, stejně mě to ponese po proudu, a to rychlostí proudu.
Toto si snad představit dovedeš.
Pokud ne, najdi si vhodnou řeku, dojdi si k ní, vem kus klacku, hoď ho do vody a podívej se co udělá.
Další situace: vesluju na klidném jezeře. Není tam žádný proud. Pojedu nějakou rychlostí vzhledem ke klidné vodě.
Když nyní začnu veslovat po proudu, rychlost, kterou bych vyvinul na klidné vodě, se přičte k rychlosti, kterou mě proud unáší.
Takže formálně (rovnoměrný přímočarý pohyb)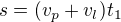
v_p - rychlost proudu
v_l - rychlost lodě na klidné vodě.
Když pojedu proti proudu, proud mě bude zpomalovat, moje rychlost způsobená veslováním se zmenší (pozorováno ze břehu) právě o rychlost proudu, takže stejnou vzdálenost pojedu delší dobu.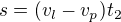
Zbytek jsou počty
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
#6 06. 03. 2020 11:51
Re: kinematika 2
Ahoj, jsem prvákem na VUT FEKT a ve Fyzice 1 jsem právě dostal tento příklad a vyřešil jsem ho. Vzhledem ke stáří diskuze ale s pěkným zpožděním asi 7 let :D. Ano, googlil jsem tento příklad jestli ho náhodou někdo neřešil přede mnou a ono opravdu řešil, naprosto stejný příklad. Trochu mi pomohl příspěvek od zdenek1, zároveň jsem si to představil i vektorově, ale nevidím tu, že by tu někdo uvedl konečné řešení této úlohy. Tak to tedy udělám já.
1) Je třeba si vyjádřit graficky, či vektorově směry rychlostí 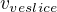 a
a 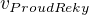 . Zkráceně bych používal
. Zkráceně bych používal  jako rychlost veslice (veslování) a
jako rychlost veslice (veslování) a 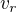 jako proud řeky.
jako proud řeky. 
- snad to bude z tohoto obrázku o trochu jasnější. Naštěstí zde operujeme pouze s osou x, takže pouze počítáme jednorozměrně.
2) Teď si to musíš představit matematicky. Takže (už podle obrázku) když pluješ po proudu, je rychlost tvého veslování doplněna o rychlost proudu řeky, který ti v tuto chvíli pomáhá. Takže plus. Když pluješ proti proudu, je rychlost tvého veslování doplněna o rychlost proudu řeky, který je v tuto chvíli tvůj nepřítel. Takže mínus. A jak už psal zdenek1, platí zde že 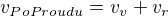 a naopak
a naopak 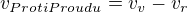 . No a teď je třeba si uvědomit, že když budeš veslovat po proudu, tak uražení vzdálenosti 120 m ti bude trvat 12 s. Zatímco když budeš veslovat proti proudu, tak uražení stejné vzdálenosti jako po proudu, tedy 120 m, akorát že na druhou stranu ti bude trvat 24 s. Tedy tyto dvě věty, co jsem právě napsal, přepiš do dvou rovnic o dvou neznámých, vycházej ale ze základního poznatku, že
. No a teď je třeba si uvědomit, že když budeš veslovat po proudu, tak uražení vzdálenosti 120 m ti bude trvat 12 s. Zatímco když budeš veslovat proti proudu, tak uražení stejné vzdálenosti jako po proudu, tedy 120 m, akorát že na druhou stranu ti bude trvat 24 s. Tedy tyto dvě věty, co jsem právě napsal, přepiš do dvou rovnic o dvou neznámých, vycházej ale ze základního poznatku, že  :
: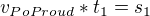

___________________________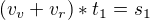
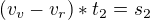 , zde zároveň platí, že
, zde zároveň platí, že 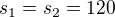 .
.
___________________________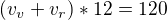
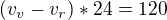
___________________________ |*2
|*2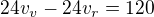
___________________________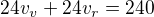
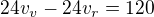 |Sčítací metoda
|Sčítací metoda
___________________________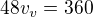 |/48
|/48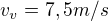 - takže to je rychlost veslování, vrátíme se do vhodné rovnice nahoře:
- takže to je rychlost veslování, vrátíme se do vhodné rovnice nahoře: |/12
|/12 |Dosaď
|Dosaď 
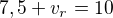 |-7,5
|-7,5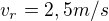 , což je proud řeky.
, což je proud řeky.
Příklad vyřešen, pro všechny, kteří by na něj někdy v budoucnu narazili.
Offline
#8 22. 03. 2020 21:59
- KennyMcCormick
- Příspěvky: 1677
- Reputace: 49
Re: kinematika 2
On nemá vlastní dotaz, napsal řešení na ten původní. 🙂
Even if you take the best course of action, the universe is still allowed to say "So what?" and kill you.
Offline

