Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#4 21. 09. 2013 22:50
Re: Počet řešení goniom. rovnice
Kosinus nabývá hodnoty 1, když je jeho argument roven  pro celé
pro celé  .
.
Platí tedy 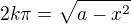 , odmocnina je vždy nezáporná, takže platí
, odmocnina je vždy nezáporná, takže platí 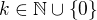 a
a 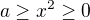 . Po umocnění máme
. Po umocnění máme 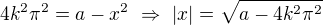 . Tato rovnice bude mít 8 řešení, když budeme mít čtyři možné výsledky odmocniny, kdyby ale byl výsledek odmocniny 0, dostaneme jen jeden kořen, proto musí platit
. Tato rovnice bude mít 8 řešení, když budeme mít čtyři možné výsledky odmocniny, kdyby ale byl výsledek odmocniny 0, dostaneme jen jeden kořen, proto musí platit 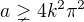 . Aby odmocnina nabývala právě čtyř hodnot, musí být
. Aby odmocnina nabývala právě čtyř hodnot, musí být 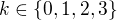 tedy
tedy  , hodnota
, hodnota  ale zas nemůže převýšit hodnotu
ale zas nemůže převýšit hodnotu  .
.
Zadaná rovnice tedy bude mít právě 8 řešení, když 
Příspěvky psané červenou barvou jsou moderátorské, šedá je offtopic.
Offline
 právě osm řešení?
právě osm řešení?
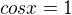 len v
len v