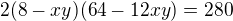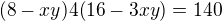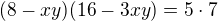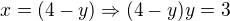Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 24. 10. 2013 12:03
Soustava rovnic :-)
Ahoj,
pokousim se prijit na kloub dalsi soustave rovnic: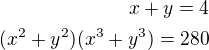
zkousim to jako ↑↑ zdenek1: zde Odkaz. Ale nemuzu to prokouknout. Ví někdo? Diky
Offline
- (téma jako vyřešené označil(a) Keeeeke)
#3 24. 10. 2013 13:20
Re: Soustava rovnic :-)
Ahoj
Maly preklep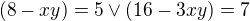
a nie
Otazka:
Ako vies, ze ide len o cele riesenia?
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#4 24. 10. 2013 13:44
Re: Soustava rovnic :-)
Ahoj, vánku. Děkuji, opraveno... a odpověď na otázku... na to se mne nikdo neptal... ;) Jen jsem pomohla s úpravou do stavu, v jakém ho chtěl tazatel mít...
Je zřejmé (už jen podle mocniny), že kořenů bude víc. Řekla bych, že další 4 (dva máme vyčerpané) v oboru komplexních čísel...
Nejsem učitelka, proto matematiku neučím, ale přímo ji řeším...
Offline
#5 24. 10. 2013 15:30
Re: Soustava rovnic :-)
↑ Keeeeke:
Až do 
se budeme držet postupu od ↑ gadgetka:
Nyní uděláme substituci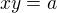
Vyřešíme si rovnici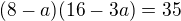
tím dostaneme i ten druhý kořen, který jí chybí
a pak postupujeme stejně
Pořádek je pro blbce, inteligent zvládá chaos!
Offline

![kopírovat do textarea $[(x+y)^2-2xy][(x+y)^3-3x^2y-3xy^2)]=280$](/mathtex/9f/9f7a67105be782763fe838d52042b559.gif)
![kopírovat do textarea $(4^2-2xy)[(4^3-3xy(x+y)]=280$](/mathtex/48/483ac59effcd185951900e535ba9cd2b.gif)