Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 30. 10. 2013 15:01 — Editoval Mythic (30. 10. 2013 15:04)
rekurentni rovnice
Ahoj,
chtěl bych poprosit, jestli by mi někdo mohl trošku dovysvětlit partikulární řešení rekurentních rovnic.
Mám zjistit jaký je vzorec pro: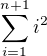
tedy: x(n+1) - x(n) = (n+1)^2
Došel jsem k řešení homogení části x(n+1) - x(n) = 0 ---> kde my vyšla báze { 1^n}
Teď bych měl řešit partikulární řešení a koukám do sešitu, že tu vždycky máme nějaký vzorec, ze kterého sme si pak vyjádřili a,b,... ale vůbec nevím jak ten řádek z kterého to budu vyjadřovat mám sestavit :(.
Offline
#2 31. 10. 2013 11:42 — Editoval Rumburak (08. 04. 2014 11:24)
Re: rekurentni rovnice
Ahoj.
Na podobný dotaz jsem už minimálně jednou odpovídal, ale nedaří se mi to najít. Podívejme se na to obecněji.
Máme-li číselné posloupnosti  ,
,  definované na množině
definované na množině  (dále jen "poslouonosti")
(dále jen "poslouonosti")
a spojené vztahem
(1) 
(kde 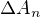 je zkratka za
je zkratka za  ) , potom posl.
) , potom posl.  nazýváme diferencí posl.
nazýváme diferencí posl.  , zatímco posl.
, zatímco posl. 
se nazývá sumace posl.  .
.
Je-li dána posl.  , pak její sumace není určena jednoznačně, avšak libovolná posl.
, pak její sumace není určena jednoznačně, avšak libovolná posl.  , která je sumací posl.
, která je sumací posl.  ,
,
se dá vyjádřit ve tvaru
(2)  ,
,
kde  je tzv. sumační konstanta charakterictická pro posl.
je tzv. sumační konstanta charakterictická pro posl.  . Tím je odůvodněn termín "sumace". Snadno nahlédneme,
. Tím je odůvodněn termín "sumace". Snadno nahlédneme,
že z (2) zpětně plyne (1) pro libovolnou posl.  a konstantu
a konstantu  .
.
("V říši" posloupností jsou pojmy diference a sumace analogií pojmů derivace a primitivní funkce "z říše" hladkých funkcí
definovaných na intervalu).
Snadno se dají dokázat vzorce
(3)  ,
, 
platné pro libovolné posl.  ,
, 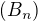 a libovolné číslo
a libovolné číslo  .
.
Od obecných úvah přejděme k posl.  pro pevně zvolenou konstantu
pro pevně zvolenou konstantu  . Z binomické věty odvodíme
. Z binomické věty odvodíme
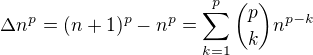 ,
,
zde pravá strana je zřejmě polynom (v proměnné  ) stupně
) stupně 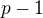 .
.
Odtud a z (3) obdržíme tvrzení:
Je-li 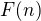 polynom stupně
polynom stupně 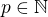 , potom
, potom 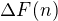 je polynom stupně
je polynom stupně 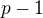 .
.
Z dosavadních úvah plyne závěr:
Je-li dán polynom  stupně
stupně 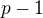 , potom funkci
, potom funkci 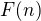 splňující vztah
splňující vztah

je rozumné hledat ve tvaru polynomu stupně  .
.
Funkci  tedy hledáme ve tvaru polynomu třetího stupně, takže
tedy hledáme ve tvaru polynomu třetího stupně, takže
(4) 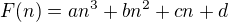 ,
,
kde konstanty 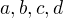 zjistíme tak, že hodnoty
zjistíme tak, že hodnoty  určíme přímo numerickým výpočtem
určíme přímo numerickým výpočtem
a dle (4) tak dostaneme soustavu čtyř rovnic o čtyřech neznámých 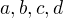 .
.
Offline