Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#4 04. 11. 2013 20:51
Re: integrál
ještě se omlouvám, ale pořád mi ten integrál vychází  ale podle výsledků i podle WA by to mělo vyjít
ale podle výsledků i podle WA by to mělo vyjít 
tady je můj postup:![kopírovat do textarea $I^2=\pi \int_{0}^{+\infty }ze^{\frac{-z}{2\sigma ^2}}dz=|f=z\Rightarrow f'=1,g'=e^{\frac{-z}{2\sigma ^2}}\Rightarrow g=-2\sigma ^2e^{\frac{-z}{2\sigma ^2}}|=\pi [z(-2\sigma ^2e^{\frac{-z}{2\sigma ^2}})]+\pi \int_{0}^{+\infty }2\sigma ^2e^{\frac{-z}{2\sigma ^2}}dz$](/mathtex/29/29720d72eb7d9aec081036bd6186f483.gif)
první výraz je roven nule, druhý když zintegruju dostanu 
počítal jsem to třikrát a pokaždý mi to vyjde stejně, nevidíte chybu?
Offline
#8 04. 11. 2013 21:25
Re: integrál
↑ Bati:
Pokud se nepletu, chybu tam má už Brano, protože v posledním kroku špatně provedl substituci (má tam být  ). Pak to vyjde správně. Rozptyl normálního rozdělení to je, ale počítal se z nenormované hustoty pravděpodobnosti, takže nevyjde
). Pak to vyjde správně. Rozptyl normálního rozdělení to je, ale počítal se z nenormované hustoty pravděpodobnosti, takže nevyjde 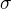 .
.
Offline
#14 04. 11. 2013 22:49
Re: integrál
↑ Hertas:
Omlouvám se, nevím jak jsem to prve kontroloval. Substituci má Brano dobře, ovšem tvůj výpočet je taky dobře. Brano tam ale chybu stejně asi mít bude, protože původní integrál vyjde takhle, zatímco odmocnina z Branova integrálu je to cos spočítal ty.
Konkrétně je mi divný krok  . V té závorce by podle mě mělo být násobení, což integrál zkomplikuje (je potřeba počítat tam integrál
. V té závorce by podle mě mělo být násobení, což integrál zkomplikuje (je potřeba počítat tam integrál  a pak udělat dvakrát per partes. Pak to nakonec vyjde správně.
a pak udělat dvakrát per partes. Pak to nakonec vyjde správně.
Asi lepší je počítat tak jak navrhoval Bati, tedy napsat to jako  , a počítat rovnou p.p. s tím, že první x se derivuje a zbytek integruje (substitucí). To je celkem rychlé.
, a počítat rovnou p.p. s tím, že první x se derivuje a zbytek integruje (substitucí). To je celkem rychlé.
No nic, čtu že už to je vyřízené, ale potom co jsem napsal nepravdu jsem si to chtěl projít celé a zkusit všechny ty možnosti. Teď už je to doufám správně.
Offline
#15 05. 11. 2013 11:41 — Editoval Brano (05. 11. 2013 11:54)
Re: integrál
↑ LukasM:
mas pravdu - pisal som to dost narychlo a chybu mam hned v tom prvom kroku
vyslo by tam  a to je na polarne suradnice nie velmi vhodne, ale da sa spocitat aj ten integral co tam uvadzas
a to je na polarne suradnice nie velmi vhodne, ale da sa spocitat aj ten integral co tam uvadzas
a potom by tam bolo aj to co si pisal povodne
totizto takyto trik sa da pouzit ked clovek pocita iba integral
(ja si vlastne ani nepamatam nejaku inu metodu nanho)
a nejak som sa asi nechal uniest, ze to musi byt podobne :-)
Offline

 , budu vděčnej za každou pomoc :)
, budu vděčnej za každou pomoc :)




 .
. ne?
ne? ale to mi přišlo zbytečný sem psát
ale to mi přišlo zbytečný sem psát ?
? a toho, že
a toho, že 
