Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 16. 11. 2013 15:04
Limita s odmocninou
Zdravím,
mám tu tento příklad. Potřeboval bych nějak popostrčit, protože mě nenapadá žádná úprava na začátek.![kopírovat do textarea $\lim_{x\to\infty } \frac{\sqrt[3]{x-5}}{2x^{3}}$](/mathtex/ed/ed5df7587e6618b8e0fae4e288e9d52d.gif)
Určitě se jedná o lehký příklad. Když si představím, jak vypadá graf čitatele a jmenovatele, tak z grafu vidím, že jmenovatel roste rychleji než čitatel, tak limita bude rovna 0.
Potřeboval bych to spíš početně vyjádřit, jak jsem došel k 0.
Děkuji za pomoc! :)
Offline
- (téma jako vyřešené označil(a) honyik)
#5 16. 11. 2013 15:31 — Editoval bejf (16. 11. 2013 15:37)
Re: Limita s odmocninou
↑ honyik:
No já bych řekl, že pod odmocninou pořád vyjde  ne? Pořád vychází po dosazení typ
ne? Pořád vychází po dosazení typ 
Edit: Pardon, máš pravdu. Ta úvaha s těma exponentama je správná. Ve jmenovateli je rychleji rostoucí funkce. Takhle je to bez L'H správně. :)
Offline

 .
. :
:![kopírovat do textarea $\lim_{x\to\infty } \frac{\sqrt[3]{x\cdot (1-\frac{5}{x})}}{2x^{3}}$](/mathtex/e1/e1f09ab68db80f9da55b4de2d78690ad.gif)
![kopírovat do textarea $\lim_{x\to\infty } \frac{x^{\frac{1}{3}}\cdot \sqrt[3]{1-\frac{5}{x}}}{2x^{3}}$](/mathtex/c7/c7115f33f2e55b7de5a6cc620066f20b.gif)
 a
a 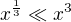 , proto
, proto  .
.