Matematické Fórum

pichucu · 20. 11. 2013 18:49

Dobrý den, dneska nám učitel zadal jako dú obrovský zlomek (přikládám obrázek) a celá třída nebo aspoň ta část s kterou komunikuju si s ním neví rady. Zkoušeli jsme obě části zlomku celé vepsat do kalkulačky a ta nám i po jejich vzájemném vydělením vyhodila obrovská čísla. Je celkem ostuda, že si třída vyššího gymnázia neví rady s takovým primitivně vypadajícím příkladem, já vím :D.
Celé znění příkladu je následující:
//forum.matweb.cz/upload3/img/2013-11/69586_Bez%2Bn%25C3%25A1zvu.png
Jakého jmenovatele bude mít zlomek?

* = znak pro násobení
3 tečky pochopitelně naznačují, že násobení jednotlivých čísel po jednom má pokračovat dál až do 100.

Brano · 20. 11. 2013 21:37 — Editoval Brano (20. 11. 2013 21:37)

urcite ti tu za chvilu niekto napise navod ako sa taketo priklady pocitaju (a nie je to ani moc tazke)
len by som zareagoval na trable s kalkulackou - na nete je super kalkulacka co sa vola Wolfram|Alpha a tam si to cislo z menovatela mozes vyratat PRESNE - inak v skratke sa zapisuje 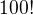$100!$
http://www.wolframalpha.com/input/?i=100%21
a teraz by ta mal zaujimat rozklad na prvocisla
http://www.wolframalpha.com/input/?i=pr … ion+100%21
cize menovatel bude skratenej formy bude $3^2=9$
alebo sa dalo rovno zadat
http://www.wolframalpha.com/input/?i=100%21%2F6%5E50
a mas vymalovane :-)

Brano · 21. 11. 2013 18:06 — Editoval Brano (23. 11. 2013 14:53)

Kedze nikto nedoplnil "bezkalkulackovy" postup, tak tu je.

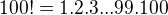Kedze v menovateli mas $6^{50}=2^{50}3^{50}$ tak potrebujes zistit kolko "dvojek" a "trojek" bude v prvociselnom rozklade $100!=1.2.3...99.100$ . Urcite za kazde parne cislo tam bude aspon jedna. Parnych cisel - t.j. delitelnych 2 tam bude $\frac{100}{2}=50$ . Lenze napr. taka "4" je delitelna dvojkou dvakrat. Cize este nam tam nejake chybaju. Kazde cislo, co je delitelne 4 sme mali zapocitat aspon 2x ale zaratali sme ho iba raz - tak ich teda pridajme este raz. Cisel delitelnych 4 je $\frac{100}{4}=25$ , lebo kazde stvrte je take. Cize sme zatial napocitali $50+25$ dvojek v prvociselnom rozklade menovatela. Ale znova 8 je delitelna dvojkou 3x a mame ju zaratanu iba 2x, tak treba este pridat vsetky cisla delitelne 8 a tych je $\frac{100}{8}=12,5$ ... 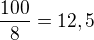no necely pocet ich nemoze byt a kedze az kazde osme je take, tak to musime zaokruhlit nadol co sa zapise takto $\left\lfloor\frac{100}{8}\right\rfloor=12$ . A takto mozme pokracovat donekonecna, len si vsimneme, ze ked uz ta mocnina dvojky v menovateli bude moc velka (vacsia ako 100) tak po zaoruhleni nadol budeme furt dostavat nuly, tak tam zastavime. Cize celkovo tych dvojek v menovateli mame $50+25+12+6+3+1=97$ .
Podobne pre pocet trojek dostaneme $\left\lfloor\frac{100}{3}\right\rfloor+\left\lfloor\frac{100}{9}\right\rfloor+...=33+11+3+1=48$ . Cize mame, ze $100!=2^{97}3^{48}n$ , pricom $n$ nie je delitelne ani 2 ani 3. A teda nas zlomok sa da upravit takto

$\frac{100!}{6^{50}}=\frac{2^{97}3^{48}n}{2^{50}3^{50}}=\frac{2^{47}n}{9}.$

Matematické Fórum

#1 20. 11. 2013 18:49

Určení jmenovatele u zajímavého zlomku.

#2 20. 11. 2013 21:37 — Editoval Brano (20. 11. 2013 21:37)

Re: Určení jmenovatele u zajímavého zlomku.

#3 21. 11. 2013 18:06 — Editoval Brano (23. 11. 2013 14:53)

Re: Určení jmenovatele u zajímavého zlomku.