Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1 2
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Vnoření L prostorů a Holderova nerovnost (TOTO TÉMA JE VYŘEŠENÉ)
#1 28. 11. 2013 19:39 — Editoval nanny1 (28. 11. 2013 20:23)
Vnoření L prostorů a Holderova nerovnost
Zdravím, mám dokázat, že pro  platí
platí  . Mám k tomu použít Holderovu nerovnost a použít za jeden člen funkci identicky rovnou 1. Mohla bych poprosit o radu? Nechci řešení, je to domácí úkol, ráda bych to vyřešila sama, ale ani nevím, jak začít.. :( Vím, co jsou prostory
. Mám k tomu použít Holderovu nerovnost a použít za jeden člen funkci identicky rovnou 1. Mohla bych poprosit o radu? Nechci řešení, je to domácí úkol, ráda bych to vyřešila sama, ale ani nevím, jak začít.. :( Vím, co jsou prostory 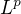 a znám předpis Holderovy nerovnosti pro tyto prostory, ale co s tím..?
a znám předpis Holderovy nerovnosti pro tyto prostory, ale co s tím..?
Co využít nějak duální prostory?
Offline
- (téma jako vyřešené označil(a) nanny1)
#3 29. 11. 2013 13:11 — Editoval nanny1 (29. 11. 2013 13:40)
Re: Vnoření L prostorů a Holderova nerovnost
Ahoj, děkuju za reakci. Omlouvám se, teď koukám, že jsem to napsala obráceně, v zadání je  . Pořád tomu moc nerozumím.. Uvažovala jsem takhle: Pro Holderovu nerovnost platí vztah
. Pořád tomu moc nerozumím.. Uvažovala jsem takhle: Pro Holderovu nerovnost platí vztah  a zároveň f.g patří do L1. Podle nápovědy si situaci zjednoduším, když položím jednu funkci rovnou jedné, napadá mě třeba f(x)=1 na intervalu <0,1>, protože
a zároveň f.g patří do L1. Podle nápovědy si situaci zjednoduším, když položím jednu funkci rovnou jedné, napadá mě třeba f(x)=1 na intervalu <0,1>, protože  . Musím tedy najít takovou funkci g(x), která patří do L1, což je "největší" prostor, použiju např. g(x)=x a norma z g(x) je tedy
. Musím tedy najít takovou funkci g(x), která patří do L1, což je "největší" prostor, použiju např. g(x)=x a norma z g(x) je tedy ![kopírovat do textarea $ (\int_{0}^{1}|x|^{q}dx)^{1/q}=\sqrt[q]{1/1+q}
$](/mathtex/41/41ad0c630c479b4435c138c4c19e4e72.gif) a na levé straně mám ten samý výsledek, ale bez odmocniny, takže nerovnost platí (jestli jsem to někde nespletla..). Ale jak teď z toho dostanu důkaz vnoření? :(
a na levé straně mám ten samý výsledek, ale bez odmocniny, takže nerovnost platí (jestli jsem to někde nespletla..). Ale jak teď z toho dostanu důkaz vnoření? :(
Offline
#8 29. 11. 2013 15:14 — Editoval nanny1 (29. 11. 2013 15:42)
Re: Vnoření L prostorů a Holderova nerovnost
Hm hm.. Záleží to na množině omega. Dělá tam neplechu nekonečno. Že by to souviselo s omezeností normy? Musíme vybrat množinu tak, aby 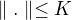 ? Ale záleží i na funkci, kterou integrujeme. Dá se to vůbec říct nějak obecně?
? Ale záleží i na funkci, kterou integrujeme. Dá se to vůbec říct nějak obecně?
Offline
#9 29. 11. 2013 15:39
Re: Vnoření L prostorů a Holderova nerovnost
↑ nanny1:
To je ono. Závisí to na tom, jestli omega má konečnou míru. To jak přesně, je napsáno třeba zde http://en.wikipedia.org/wiki/Lp_space#Embeddings . K důkazu potom můžeš použít toho Holdera (uvědom si, kdy je jednotková funkce integrovatelná), ale lze to i elementárněji, když z intergálů odřízneš množinu, kde integrovaná funkce je větší než jedna, a pak odhadneš, zhruba řečeno.
Offline
#11 30. 11. 2013 17:13
Re: Vnoření L prostorů a Holderova nerovnost
Přiznám se, že si nejsem jistá, co je jednotková funkce.. Myslíš f(x)=1? Pak na měřitelných množinách je integrál 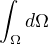 mírou množiny omega (jestli si to myslím dobře.. Míru a Lebesgueův integrál budu mít až za dva roky). Ta Holderova nerovnost, kterou jsem psala předtím - je prosím ten postup aspoň nějak dobře? Jenom to musím napsat obecně pro libovolnou měřitelnou množinu, nemůžu asi použít konkrétní interval <0,1>, i když by se zrovna hodil...
mírou množiny omega (jestli si to myslím dobře.. Míru a Lebesgueův integrál budu mít až za dva roky). Ta Holderova nerovnost, kterou jsem psala předtím - je prosím ten postup aspoň nějak dobře? Jenom to musím napsat obecně pro libovolnou měřitelnou množinu, nemůžu asi použít konkrétní interval <0,1>, i když by se zrovna hodil...
Offline
#13 30. 11. 2013 17:27
Re: Vnoření L prostorů a Holderova nerovnost
No on se tenhle předmět zapisuje až ve vyšším ročníku, zapsala jsem si to už teď a jsem z toho taky pěkně vykulená. :D Míra a integrál je pak předmět na celej semetr. Něco jsem si přečetla, snad základy znám.
Offline
#15 30. 11. 2013 18:03
Re: Vnoření L prostorů a Holderova nerovnost
↑ nanny1:
Tipuju, že to je z funkcionální analýzy?
Ona ta funkční hodnota vlastně v Lebesgueovo integrálu může mít konečný počet výjimek.
Dokonce spočetný počet. Prvky prostoru Lp jsou ve skutečnosti třídy ekvivalence, která říká, že 2 funkce jsou si ekvivalentní, pokud se rovnají skoro všude (tedy až na množiny Lebesgueovy míry 0, což jsou všechny spočetné množiny, ale i některé nespočetné, viz. Cantorova).
Co se týče toho důkazu, nechce se mi to sem celé psát. Zkus začít tak, že si řekneš, že ta funkce patří do menšího prostoru a pokusíš se ukázat, že je taky v tom větším, a pak to sem napiš, kam jsi došla.
Offline
#22 05. 12. 2013 10:31
Re: Vnoření L prostorů a Holderova nerovnost
Já si myslím, že to musí jít i jinak a míň komplikovaně. Navíc si u pár věcí nejsem jistá, jestli jsou úplně košer. Každopádně jsem na levé stravě potřebovala místo jednotkové normy absolutní hodnotu na p-tou, našla jsem tu rovnost (která je mi teda taky divná..), dosadila jsem za integrál součinu  (celou nerovnost jsem předtím umocnila na p-tou), vynásobila tou mírou na (1-p), tím jsem na pravé straně dostala míru na (2-p) a dosazením q=p/(p-1) mi vyšel ten konečný tvar.
(celou nerovnost jsem předtím umocnila na p-tou), vynásobila tou mírou na (1-p), tím jsem na pravé straně dostala míru na (2-p) a dosazením q=p/(p-1) mi vyšel ten konečný tvar.
Offline
Stránky: 1 2
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Vnoření L prostorů a Holderova nerovnost (TOTO TÉMA JE VYŘEŠENÉ)


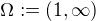 . Pak zřejmě
. Pak zřejmě 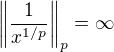 , ale
, ale  .
. 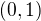 .
. 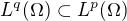 , když platí
, když platí 
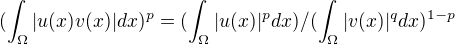
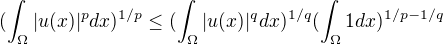 , což znamená, že prostory jsou vnořené.
, což znamená, že prostory jsou vnořené.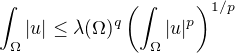 ,
, .
. 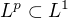 pro všechna
pro všechna  . Teď jde o to, jestli to jde nějak převést na
. Teď jde o to, jestli to jde nějak převést na 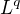 ,
,  .
.