Matematické Fórum

Booback · 05. 12. 2013 12:59

Ahoj, prosím muže mi někdo poradit, jak vypočítat tento příklad?
//forum.matweb.cz/upload3/img/2013-12/44629_Sn%25C3%25ADmek%2Bobrazovky%2B2013-12-05%2Bv%25C2%25A012.55.58.png Ve škole to neberem, ale mám to jako dú a na netu jsem nenašla nic, co by mi to pomohlo pochopit.

Brano · 05. 12. 2013 13:46 — Editoval Brano (05. 12. 2013 13:46)

↑ Booback:
Ten priklad je zle zadany, lebo ta sustava nema ZIADNE riesenie a teda sa neda hladat ani priblizne.

Ale ked sa teda odosobnime od neschopnosti zadavatela forrmulovat zadanie korektne, tak to co sa tym zrejme mysli je toto:
Najdite take 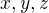$x,y,z$ , aby sucet kvadratov odchyliek 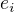$e_i$ bol minimalny, kde 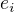$e_i$ su definovane v
$x-y+z=1+e_1$ , $2x+y+z=2+e_2$ , $x-2y-2z=-1+e_3$ , $-x-y-z=e_4$ ,
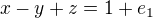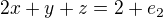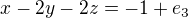alebo inymi slovami hladas bod minima funkcie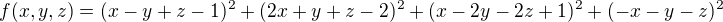

$f(x,y,z)=(x-y+z-1)^2+(2x+y+z-2)^2+(x-2y-2z+1)^2+(-x-y-z)^2$
co sa najde lahko - tu je vysledok pre kontrolu.

Booback · 05. 12. 2013 16:47

↑ Brano:
děkuji moc, já si právě nevěděla rady, jelikož nám k tomu ve škole nic neřekli a že to nebude ani na zk, ale je to dú za bod, takže opravdu děkuju ;) každý bod se hodí :)

Matematické Fórum

#1 05. 12. 2013 12:59

metoda nejmenších čtverců

#2 05. 12. 2013 13:46 — Editoval Brano (05. 12. 2013 13:46)

Re: metoda nejmenších čtverců

#3 05. 12. 2013 16:47

Re: metoda nejmenších čtverců

Zápatí