Matematické Fórum

Katka1994

Dobrý den, prosím, zkontroloval by mi někdo celý příklad, zda-li ho mám správně? Postup i všechna čísla a výpočty? Předem moc děkuji za pomoc! :-)

Ve kterém bodě má parabola $y=2x^{2}+3x-1$ tečnu
a) se směrovým úhlem 45°
b) rovnoběžné s přímkou 5x - y + 3 = 0
c) kolmou na přímku x - 3y + 2 = 0

a) se směrovým úhlem 45°

Musím si uvědomit, že směrnice je tangens úhlu, který svírá přímka s kladnou částí osy x, proto $\text{tg}45^\circ =1$ a musím si uvědomit, že směrnice je rovna první derivaci funkce.

$(2x^{2}+3x-1)'=\text{tg}45^\circ$

$2x+3=1$ ... takže první souřadnice bodu je $x=-1$

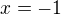
Získanou souřadnici dosadíme do předpisu paraboly $2(-1)^{2}+3(-1)-1=-2$ , takže tečnu má v bodě $T[-1,-2]$

b) rovnoběžné s přímkou 5x - y + 3 =0

Přímku si upravím na směrnicový tvar $y=5x+3$ a platí, že přímky jsou navájem rovnoběžné, když mají stejnou směrnici, proto první derivace funkce bude rovna směrnici zadané přímky.

$(2x^{2}+3x-1)'=5$

$2x+3=5$ ... takže první souřadnice bodu je $x=1$

Získanou souřadnici dosadíme do předpisu paraboly $2+3-1=4$ , takže tečnu má v bodě $T[1,4]$

c) kolmou na přímku x - 3y + 2 = 0

Přímku si upravím na směrnicový tvar $y=\frac{1}{3}x+\frac{2}{3}$ a platí, že přímky jsou navzájem kolmé právě tehdy, když pro jejich směrnice platí vztah $k_{2}=-\frac{1}{k_{1}}$ ...

Směrnice kolmé přímky bude $k_{2}=-\frac{1}{\frac{1}{3}}=-3$ a získana směrnice bude rovna první derivaci předpisu funkce.

$(2x^{2}+3x-1)'=-3$

$2x+3=-3$ ... takže první souřadnice bodu je $x=0$

Získanou souřadnici dosadíme do předpisu paraboly $0+0-1=-1$ , takže tečnu má v bodě $T[0,-1]$

vanok · 10. 12. 2013 17:13

Ahoj ↑ Katka1994:,
Mas chybu nepozornosti v tvojej derivacii
$(2x^{2}+3x-1)'=\text{tg}45^\circ$
Da
$2.2x+3=...$
( vyskocila ti tam jedna 2)

Katka1994 · 10. 12. 2013 17:14

↑ vanok:

Děkuji moc!! Celé si to přepočítám :-)

Katka1994 · 10. 12. 2013 17:19

↑ vanok:

část a)

$4x+3=1$

$x=-\frac{1}{2}$

Takže souřadnice bodu $T[-\frac{1}{2},-2]$

část b)

$4x+3=5$

$x=\frac{1}{2}$

Takže souřadnice bodu $T[\frac{1}{2},1]$

část c)

nijak má chyba neovlivní ..

je tak? :-)

Matematické Fórum

#1 10. 12. 2013 16:22 — Editoval Katka1994 (10. 12. 2013 16:59)

Tečna paraboly (derivace)

#2 10. 12. 2013 17:13

Re: Tečna paraboly (derivace)

#3 10. 12. 2013 17:14

Re: Tečna paraboly (derivace)

#4 10. 12. 2013 17:19

Re: Tečna paraboly (derivace)

Zápatí