Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 21. 12. 2013 16:06
- check_drummer

- Příspěvky: 5447
- Reputace: 106
Chladnutí kávy
Ahoj,
jedna úloha z praxe (není zadána zcela přesně, rozmné předpoklady si doplňte prosím sami):
V čase t=0 se dovaří voda a je zalita káva v hrníčku tak, že 2/3 objemu hrníčku tvoří horká voda. Kávu chci zalít mlékem (mléko má teplotu místnosti), tak, abych naplnil celý hrníček, ale nechci ji pít ihned, ale v čase t=t1. Otázka zní, zda je lepší zalít vodu mlékem ihned v čase t=0 nebo zda se zalitím počkat až do času t=t1 nebo za to nehraje roli. V čase t1 chci mít co nejteplejší kávu. Další otázka je, zda se odpověď změní, pokud mléko bude mít jinou teplotu než pokojovou (intuitivně by mohlo, protože tím, že jej naleju do hrníčku, stane se součástí pokoje).
Pozn.: Rozumnými předpklady jsem myslel např. předpklady o výměně tepla mezi hrníčkem a okolním prostředím (místností).
"Máte úhel beta." "No to nemám."
Online
#2 24. 12. 2013 23:18
Re: Chladnutí kávy
↑ check_drummer: Ahoj, pekný príklad si zadal :-) ... ale každým okamžikom nám nespútané fotóny unikajú do vesmíru... to čo sme nazhromaždili varom do objemu tak každým kúskom času nenávratne mizne v temnote....
najteplejšiu kávu máme hneď po zvarení... to mám odskúšané..ale na konzum by bolo tak vhodné cca 37stC?
Výhodné by to bolo riešiť graficky
pozrime napr. Obr 7
Offline
#3 10. 04. 2018 06:22
Re: Chladnutí kávy
↑ check_drummer:
Ahoj, takové důležité téma zůstalo nevyřešené!
Přesvědčil jsem se, že pro splnění zadání je potřeba mléko přidat co šálku co nejdřív, nejlépe ještě před kávou. Pokusím se k tomu něco naznačit. Použiju hodně zjednodušující předpoklady, bude-li někdo chtít, může to případně rozšířit či upřesnit.
Vyjdu z rovnice pro tepelné ztráty přestupem tepla: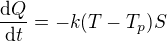 , neboli
, neboli 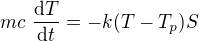
 je hmotnost tělesa
je hmotnost tělesa je měrné teplo tělesa
je měrné teplo tělesa je teplota chladnoucího tělesa
je teplota chladnoucího tělesa je součinitel přestupu tepla
je součinitel přestupu tepla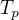 je teplota okolního prostředí
je teplota okolního prostředí je povrchová plocha tělesa
je povrchová plocha tělesa
Budeme předpokládát, že káva vydává teplo do okolí celým svým povrchem  stejně, zanedbáme ochlazování v důsledku odpařování. Prostorové rozložení teploty kávy i okolního prostředí považujeme za konstantní.
stejně, zanedbáme ochlazování v důsledku odpařování. Prostorové rozložení teploty kávy i okolního prostředí považujeme za konstantní.
Řešením výše uvedené rovnice je teplota jako funkce času: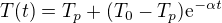
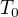 je počáteční teplota
je počáteční teplota je časová konstanta, pro kterou platí
je časová konstanta, pro kterou platí 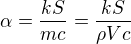
 je měrná hustota kávy
je měrná hustota kávy je objem kávy
je objem kávy
Aby bylo možné pokračovat, je třeba znát souvislost mezi povrchem  a objemem
a objemem  a odhadnout součinitel přestupu tepla
a odhadnout součinitel přestupu tepla  . Můžeme si zvolit například tvar válce, jehož výška je stejná jako jeho průměr. Pak lze provést dvě varianty výpočtu: smíchání+chladnutí resp. chladnutí+smíchání.
. Můžeme si zvolit například tvar válce, jehož výška je stejná jako jeho průměr. Pak lze provést dvě varianty výpočtu: smíchání+chladnutí resp. chladnutí+smíchání.
Offline
#4 10. 04. 2018 08:17 — Editoval MichalAld (10. 04. 2018 08:18)
Re: Chladnutí kávy
↑ medvidek:
Jo jo, přesně jak píšeš (i když všechny detaily těch výpočtů jsem nekontroloval).
Přijde mi to celkem zřejmé i bez počítání - výsledná teplota kávy je určena počátečními vlastnostmi (teplota, hmotnost, tepelná kapacita) těch věcí, ze kterých se to udělá (káva, voda, mléko, hrnek), a teplem, které během procesu odejde do okolí.
A je myslím celkem zřejmé, že čím bude hrnek s kávou teplejší, tím více tepla odevzdá do okolí, a co odevzdá, už nikdy zpět nedostane.
Jediná věc, která by v principu předchozí tvrzení mohla zhatit je přenos tepla prouděním. Kolem hrnku se vytvoří vzdušný proud, který přispívá k ochlazování (a nakonec i v hrnku s kávou to bude proudit) - a nelze nějak jednoduše dokázat, že nemůže za jistých podmínek nastat inverzní situace- že při trochu nižší teplotě bude proudění odvádět více tepla než při vyšší.
Na proudění tekutin je zatím matematika krátká - je to nakonec jeden ze sedmi "matematických problémů tisíciletí" - řešení Navier-Stokesovy rovnice.
Nejlepší by tedy bylo tam nalít mlíko ještě dřív než vodu, ale asi by se to pak nedalo pít (zejména v případě turecké kávy). Já mám tedy doma inverzní problém, aby káva vychladla co nejrychleji, takže jsem přesně tuhle úlohu taky kdysi řešil. Nakonec se ale ukázalo, že zcela nejlepší řešení je přesvědčit manželku, aby mi ji zalila půl hodky před tím, než se vyhrabu z postele, hi.
Online
#5 10. 04. 2018 09:03
Re: Chladnutí kávy
↑ MichalAld:
Pozdravuju manželku :)
Ta inverze mě nenapadla. A i kdyby, ihned bych ji zanedbal.
Intuitivně jsem to bral jako jasnou věc, ale je tam jeden faktor, který částečně působí "proti":
Buď máme velký povrch méně teplý, anebo malý povrch, který je teplejší. Samozřejmě to velmi záleží na vlastnostech hrnku.
Mohu říct, že v mém šálku proudí káva docela dobře. Když jsem měřil teplotu chladnutí, rozdíly nikdy nebyly větší než jeden stupeň. Dá se namítnout, že k určitému míchání teploměrem mohlo docházet, ale spíš si myslím, že k proudění dochází v důsledku ochlazování na hladině.
Offline
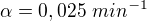 , zatímco při 2/3 naplnění byla rychlost
, zatímco při 2/3 naplnění byla rychlost 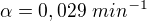 .
. 