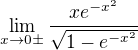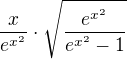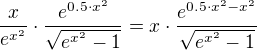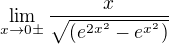Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 22. 12. 2013 20:08 — Editoval Aktivní (22. 12. 2013 20:59) Příspěvek uživatele Sherlock byl skryt uživatelem Aktivní.
#3 22. 12. 2013 20:16 — Editoval Aktivní (22. 12. 2013 20:31) Příspěvek uživatele Sherlock byl skryt uživatelem Aktivní. Důvod: blbost
#4 22. 12. 2013 21:21
Re: Jednostranné limity
Aktivní napsal(a):
Ten spodek se dá upravit:
Vznikne z toho součin
Ten se dá upravit
a dál
Poznámka: Ten členje lichý, a tak se nesmí dát pod tu odmocninu, stal by se z něho sudý člen, aneb úprava
je ekvivalentní jenom pro kladná x. Mohl by se k tomu vyjádřit někdo znalejší.
Offline
#5 22. 12. 2013 23:04 — Editoval Jj (22. 12. 2013 23:05)
Re: Jednostranné limity
↑ Mirgeee:
Dobrý večer, řekl bych, že asi lze uvažovat i takto:
Funkce  je lichá, takže bude platit
je lichá, takže bude platit 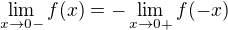 ,
,
je tudíž možno počítat jen jednostrannou limitu pro 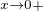 , to zn. pro x > 0, což výpočet
, to zn. pro x > 0, což výpočet
zjednodušší (viz problém uvedený kolegou ↑ Aktivní:):
 na výraz pod odmocninou užít L'Hospitala
na výraz pod odmocninou užít L'Hospitala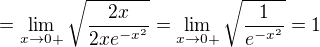 , čili limita zleva = -1.
, čili limita zleva = -1.
Pokud se tedy nemýlím.
Offline