Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Zajímavé středoškolské úlohy
- » Pekná a známa teória čísel (TOTO TÉMA JE VYŘEŠENÉ)
#1 23. 12. 2013 18:47
Pekná a známa teória čísel
Nech  je prirodzené číslo. Dokážte, že ak
je prirodzené číslo. Dokážte, že ak  je prirodzené číslo, tak je to štvorec celého čísla.
je prirodzené číslo, tak je to štvorec celého čísla.
Napríklad:
Pre 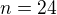 platí
platí  .
.
Pre  platí
platí 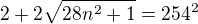 .
.
1^6 - 2^6 + 3^6 = 666
Offline
- (téma jako vyřešené označil(a) BakyX)
#2 02. 01. 2014 23:29 — Editoval liamlim (03. 01. 2014 20:15)
Re: Pekná a známa teória čísel
Po dlouhé době jsem se díval na fórum. možná to mám špatně, ale přesto napíšu.
Offline
#3 03. 01. 2014 07:37
Offline
Stránky: 1
- Hlavní strana
- » Zajímavé středoškolské úlohy
- » Pekná a známa teória čísel (TOTO TÉMA JE VYŘEŠENÉ)

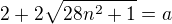 pro nějaké přirozené
pro nějaké přirozené  . Tuto rovnost pak upravím na tvar
. Tuto rovnost pak upravím na tvar 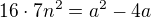 . Podle zbytků lze snadno odvodit že 4 dělí
. Podle zbytků lze snadno odvodit že 4 dělí  pro nějaké přirozené
pro nějaké přirozené  . Pak platí rovnost
. Pak platí rovnost  .
. pro přirozené
pro přirozené  . Pak platí
. Pak platí  neboli
neboli 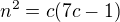 . Ze zřejmé nesoudělnosti
. Ze zřejmé nesoudělnosti 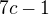 vidíme, že musí nutně být
vidíme, že musí nutně být  přirozené tedy platí
přirozené tedy platí 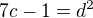 což dává
což dává  . Toto ale nedává smysl, protože druhá mocnina přirozeného čísla nemůže mít při dělení 7 zbytek 6. Našli jsme tedy hledaný spor.
. Toto ale nedává smysl, protože druhá mocnina přirozeného čísla nemůže mít při dělení 7 zbytek 6. Našli jsme tedy hledaný spor. 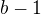 . Tedy existuje přirozené
. Tedy existuje přirozené 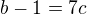 neboli
neboli  . Po dosazení máme
. Po dosazení máme  neboli
neboli  . Vzhledem ke zřejmé nesoudělnosti
. Vzhledem ke zřejmé nesoudělnosti 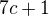 musí být obě tato čísla druhými mocninami. Existuje tedy přirozené
musí být obě tato čísla druhými mocninami. Existuje tedy přirozené  . Pak z rovností
. Pak z rovností 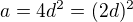 . Tímto je důkaz hotov.
. Tímto je důkaz hotov.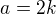 , z čoho následne po umocnení ľahko vidieť, že aj
, z čoho následne po umocnení ľahko vidieť, že aj  je párne. Super
je párne. Super