Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 29. 12. 2013 16:29 — Editoval CLieR (29. 12. 2013 18:11)
Nejmenší hodnota výrazu
Dobrý den,
mám zadán výraz V(a,b), po úpravě dostávám:
a) Urči nejmenší hodnotu výrazu V pro 
b) Urči nejmenší hodnotu výrazu V pro 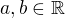
c) Urči všechna čísla  , pro která je V = 2013
, pro která je V = 2013
Potřeboval bych jen navést, děkuji.
P.S. Výraz samotný byl na začátku složitější (podíl zlomků s odmocninami), v případě nutnosti ho samozřejmě mohu dodat.
Příklad č. 2:
Mám zadán pravidelný komolý čtyřboký jehlan, znám délku horní i dolní podstavy a také tělesové úhlopříčky. Jak určit poloměr kulové plochy opsané tímto jehlanem?
Offline
#9 04. 01. 2014 15:00
Re: Nejmenší hodnota výrazu
Děkuji, samozřejmě jsem dělal opakovaně chybu u násobení třetích odmocnin, jinak vše stejně.
ohledně d) V(a,b) = 2013 jsem zvolil tento postup:
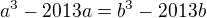
Což platí pro a=b, tudíž nevyhovující podmínkám. Korektní postup?
Ohledně mého původního dovětku s jehlanem - již vyřešeno :).
Děkuji.
Offline

![kopírovat do textarea $
\frac{a^{\frac{3}{2}} + b^{\frac{3}{2}}}{(a^2 - ab)^\frac{2}{3}} : \frac{\sqrt[3]{\frac{1}{a} - \frac{b}{a^2}}}{a\sqrt{a} - b\sqrt{b}}
$](/mathtex/51/51b9efa6d2bc2e5778b947d62085b49b.gif)


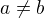


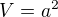
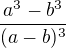 , což je
, což je 
![kopírovat do textarea $\frac{a^{\frac{3}{2}} + b^{\frac{3}{2}}}{(a^2 - ab)^\frac{2}{3}} : \frac{\sqrt[3]{\frac{1}{a} - \frac{b}{a^2}}}{a\sqrt{a} - b\sqrt{b}}=\frac{a\sqrt a+b\sqrt b}{\sqrt[3]{a^2(a-b)^2}}\cdot \frac{a\sqrt a-b\sqrt b}{\sqrt[3]{\frac{a-b}{a^2}}}=\frac{a^3-b^3}{\sqrt[3]{\frac{a^2(a-b)^3}{a^2}}}=\frac{(a-b)(a^2+ab+b^2)}{a-b}=a^2+ab+b^2$](/mathtex/21/216cc11dd09ed5e2c64ceb99770413d1.gif)