Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy z matematické analýzy
- » Hledání funkce (TOTO TÉMA JE VYŘEŠENÉ)
#1 19. 02. 2009 14:11
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Hledání funkce
Poslední dobou se tu toho moc neděje, tak bych přidal něco na způsob funkcionální rovnice, taková úloha tu pokud vím ještě nebyla.
Najděte všechny funkce
takové, že
Je to úloha z mezinárodní matematické olympiády (samozřejmě ne aktuální, takže můžete řešit :-).
Offline
#2 19. 02. 2009 15:04
Re: Hledání funkce
Zatím jsem dokázal toto:
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#3 25. 02. 2009 22:45
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Hledání funkce
Zatím žádné kompletní řešení, zkusím vás trochu povzbudit ... :-)
Snad vás neodradilo to, že se jedná o úlohu z mezinárodní matematické olympiády. Neřekl bych, že je tato úloha nějak zvlášť těžká (pokud bych měl srovnat obtížnost s úlohami od Mariana, tak bych ji řadil mezi ty jednodušší), nechci tedy zatím uvádět žádnou nápovědu...
Offline
#4 26. 02. 2009 00:10
Re: Hledání funkce
↑ BrozekP:
Já ti nevím :) Táto časť fóra zrejme nie je až taká populárna až na niektorých. Ja teda neviem ako by som na to mal ísť, pretože nemám skúsenosti z nejakých súťaží. Je to typ úloh za ktorými vidím len písmená, teda ako keď čítam odborný článok z jadrovej fyziky :( Neviem teda nejaký spôsob ako začať, možno by sa hodila nápoveda aj keď bola úloha zadaná relatívne nedávno. Raz som takú jednoduchšiu úlohu videl, že si tam riešiteľ zvolil nejakú "šablónovú" funkciu a podľa podmienok hľadal koeficienty, lenže ja neviem ako si ju mám zvoliť. Príde mi to také veľmi sofistikované...
"The mathematical rules of the universe are visible to men in the form of beauty."
John Michel
Offline
#5 26. 02. 2009 09:49 — Editoval BrozekP (26. 02. 2009 09:53)
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Hledání funkce
↑ lukaszh:
Řešitel si nemůže zvolit jen tak nějakou "šablonovou" funkci, to by mohl přijít o spoustu řešení. K tomu, aby se mohl zabývat jen určitým typem funkcí, musí mít dobrý důvod. V zadání snad není pro tebe nic nesrozumitelného, jen si asi potřebuješ uvědomit, co to vlastně říká. Zkus se procvičit na jiné úloze :-)
Najděte všechny funkce
takové, že
Úlohy u kterých člověk ví jak na ně hned od začátku přece nejsou zajímavé. Nejlepší je, když člověk sám objeví způsob, jak se nějaká úloha řeší.
Offline
#6 26. 02. 2009 20:26
Re: Hledání funkce
↑ BrozekP:
Možno takým sedliackym úsudkom to je konštantná funkcia f(z)=1.
"The mathematical rules of the universe are visible to men in the form of beauty."
John Michel
Offline
#7 26. 02. 2009 22:05
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Hledání funkce
↑ lukaszh:
No dobře, ale zkus to nějak matematicky bez selského rozumu :-)
Offline
#8 26. 02. 2009 23:03
Re: Hledání funkce
↑ BrozekP:
Vychádzam z rovnosti
Môžem všeobecne zapísať riešenia
Lenže odtiaľ priamo vyplýva závislosť hodnoty f(x) od hodnoty f(y), tu by som videl problém, že už nevyplýva voľba ľubovoľného čísla x, ale takého, ktoré odpovedá hodnote y v rovnici. Preto hľadám funkciu f(z), ktorá nezávisí od voľby x,y teda iba konštantná f(z) = c. Hľadám konštantu aby platilo
"The mathematical rules of the universe are visible to men in the form of beauty."
John Michel
Offline
#9 27. 02. 2009 12:36
Re: Hledání funkce
↑ lukaszh:
Co tak zvolit 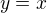 ? Pak
? Pak
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#11 27. 02. 2009 14:13 — Editoval Pavel (27. 02. 2009 14:18)
Re: Hledání funkce
↑ andrew:
Dosadil jsem  do funkcionální rovnice a dostal jsem
do funkcionální rovnice a dostal jsem
Takže buď  nebo
nebo  . Z předpokladů vyplývá, že
. Z předpokladů vyplývá, že  pro
pro  . Takže nemůže platit
. Takže nemůže platit  - není jiná možnost, než že
- není jiná možnost, než že  . Použiju-li stejný předpoklad ještě jednou, dostanu
. Použiju-li stejný předpoklad ještě jednou, dostanu  pro
pro  . Aby
. Aby  , není jiná možnost, než že
, není jiná možnost, než že  , a tedy
, a tedy  .
.
Z tvého řešení by vyplývalo, že 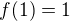 , ale
, ale
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#13 27. 02. 2009 15:07 — Editoval Pavel (27. 02. 2009 15:09)
Re: Hledání funkce
↑ andrew:
Já bych si dal pozor na implikaci
Nikde není psáno, že jediné reálné číslo, v němž je funkční hodnota 0, je x=2. Není těžké ukázat, že 
Tudíž ta implikace  nemusí platit.
nemusí platit.
Z předpokladu 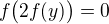 může stejně tak vyplývat, že
může stejně tak vyplývat, že  jako
jako  :-)
:-)
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#14 27. 02. 2009 16:41
Re: Hledání funkce
↑ Pavel:
Nikde není psáno, že jediné reálné číslo, v němž je funkční hodnota 0, je x=2. Není těžké ukázat, že 
Vsimni se, ze abych mohl psat 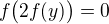 musim predpokladat
musim predpokladat  . A to je pro jake hodnoty
. A to je pro jake hodnoty  pravda? Samozrejme, ze jen pro
pravda? Samozrejme, ze jen pro  dle bodu
dle bodu  . Takze se pri hledani
. Takze se pri hledani  pohybuju na intervalu
pohybuju na intervalu  nikoliv vsak na
nikoliv vsak na  .
.
Samozrejme vim, ze plati  . Jedine co nevim, je jak vypada
. Jedine co nevim, je jak vypada  na
na  . Dale z bodu
. Dale z bodu  plyne
plyne  . Odtud
. Odtud 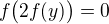 a z bodu
a z bodu  dostavam
dostavam  a tedy
a tedy  .
.
Offline
#15 27. 02. 2009 23:46
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Hledání funkce
↑ andrew:
Uvažujme pouze  . Pak
. Pak  . Ale stále nic nevíme o tom, kolik
. Ale stále nic nevíme o tom, kolik  je, nevíme tedy jestli
je, nevíme tedy jestli  je z intervalu [0,2], víme pouze, že je to nezáporné číslo. Nemůžeme tedy přejít na interval [0,2] tak, jak to děláš. Jestliže platí
je z intervalu [0,2], víme pouze, že je to nezáporné číslo. Nemůžeme tedy přejít na interval [0,2] tak, jak to děláš. Jestliže platí  , pak klidně může být
, pak klidně může být  . Myslím, že to jasně napsal Pavel ve svém příspěvku.
. Myslím, že to jasně napsal Pavel ve svém příspěvku.
Offline
#16 07. 03. 2009 22:33
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Hledání funkce
Offline
#17 24. 03. 2009 12:11
Re: Hledání funkce
↑ BrozekP:
Tak mám rešení. Není nadto řešit takovéto úlohy ve vlaku :-) (Marian potvrdí :-) )
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#18 24. 03. 2009 20:46
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Hledání funkce
Offline
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy z matematické analýzy
- » Hledání funkce (TOTO TÉMA JE VYŘEŠENÉ)




 ? Me vyslo
? Me vyslo 
 . Ja si zvolil
. Ja si zvolil  a po dosazeni mam
a po dosazeni mam  . Z bodu
. Z bodu 
 , pak
, pak  , kde
, kde  . Z i) a ii) vyplývá, že
. Z i) a ii) vyplývá, že , a tedy
, a tedy 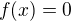 pro
pro  .
. , a tudíž výraz
, a tudíž výraz  má smysl. Položme tedy
má smysl. Položme tedy  . Pak z i) plyne, že
. Pak z i) plyne, že
 .
.
 . Ze stejného důvodu jako v první části musí platit, že
. Ze stejného důvodu jako v první části musí platit, že .
. .
.