Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 15. 01. 2014 10:36
Homeomorfismus
Dobrý den, prosím o pomoc s důkazem následující věty:
Buď f bijekce topologického prostoru X na topologický prostor Y. Potom následující výroky jsou ekvivalentní:
1) f je homeomorfismus
2) Pro každou množinu A, která je podmnožinou X, platí, že obraz jejího vnitřku v X je vnitřek v Y obrazu množiny A.
Kdyby byla A otevřená, tak to chápu. Obraz otevřené množiny je otevřená množina. Ale s uzavřenou si nevím rady...
Offline
- (téma jako vyřešené označil(a) Polopat)
#2 15. 01. 2014 10:57 — Editoval Rumburak (15. 01. 2014 11:27)
Re: Homeomorfismus
↑ Polopat:
Zdravím .
Obecná podmnožina A topologického prostoru X ho rozdělí na 3 disjunktní části (některé mohou být prázdné), jimiž jsou
- vnitřek množiny A ,
- vnitřek množiny X-A ,
- hranice množiny A (= hranice množiny X-A).
Ta poslední je uzavřená, ostatní jsou otevřené. Stačí tato nápověda ?
Offline
#4 15. 01. 2014 11:48
Re: Homeomorfismus
↑ Rumburak:
Bohužel se v tom ztrácím. Každá myšlenka mě vždycky zavede jenom k tomu, že obraz otevřené je otevřená a uzavřené uzavřená. Že obraz vnitřku A leží v obrazu A je mi jasné, ale že je roven vnitřku toho obrazu, k tomu nevím vůbec jak dojít. Zkoušel jsem aplikovat totéž třeba v opačném směru, ale vždy jsem se v tom nějak ztratil...
Offline
#5 15. 01. 2014 12:17 — Editoval Rumburak (15. 01. 2014 12:17)
Re: Homeomorfismus
↑ Polopat:
Ten důkaz nebude možno provést úplně šmahem už proto, že máme dokázat ekvivalenci dvou výroků, konkretně výroků
(1) f je homeomorfismus ,
(2) pro každou množinu A, která je podmnožinou X, platí, že obraz jejího vnitřku v X je vnitřek v Y obrazu množiny A,
tedy dvě implikace
I. (1) implikuje (2) ,
II. (2) implikuje (1) .
Nejprve se tedy musíme rozhodnout, s kterou z těchto dvou částí začneme a na tu se zaměřit.
Offline
#6 15. 01. 2014 13:52
Re: Homeomorfismus
Poznamka
Je dobre pripomenut definiciu homeomorfismu:
http://en.wikipedia.org/wiki/Homeomorphism
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#7 16. 01. 2014 14:42 — Editoval Brano (16. 01. 2014 14:42)
Re: Homeomorfismus
Mozem napisat nejake hinty, aby sa to pohlo: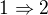
Pre  uvazujme
uvazujme  a
a 
chces dokazat, ze  - co sa da rozbit na dva kroky
- co sa da rozbit na dva kroky a
a  .
.
Chces dokazat, ze  je spojite a otvorene. Dokazat, ze je otvorene je trivialne. Na spojitost mozes ist sporom. Predpokladaj, ze mame
je spojite a otvorene. Dokazat, ze je otvorene je trivialne. Na spojitost mozes ist sporom. Predpokladaj, ze mame 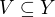 otvorenu taku, ze
otvorenu taku, ze 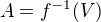 nie je otvorena. Zamysli sa co potom z toho vyplyva pre
nie je otvorena. Zamysli sa co potom z toho vyplyva pre 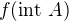 .
.
Offline
#8 16. 01. 2014 22:20
Re: Homeomorfismus
↑ Brano:
Omlouvám se, že jsem se neozýval, nebyl čas.
Jinak jsem si řekl, že obraz vnitřku A je podmnožina obrazu A. Obraz vnitřku A je ale otevřená množina, takže je roven vnitřku obrazu vnitřku A. Vnitřek je největší otevřená podmnožina, takže vnitřek obrazu A nemůže být "menší" než vnitřek obrazu vnitřku A, tudíž je nadmnožinou. Opačná inkluze by se dokázala analogicky. Je to tak?
Na druhou implikaci se ještě podívám. Děkuji za trpělivost.
Offline
#10 17. 01. 2014 11:48
Re: Homeomorfismus
↑ Polopat:
skoro, ale ides na to dobre - vyuzivame to, ze homeomorfizmus zobrazuje otvorene mnoziny na otvorene v oboch smeroch.
kedze 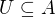 , tak aj
, tak aj 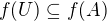 , lenze
, lenze 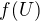 je otvorena a teda
je otvorena a teda  (z toho dovodu co si napisal, len zatial nemame rovnost)
(z toho dovodu co si napisal, len zatial nemame rovnost)
uplne rovnakym argumentom dostaneme  a na obe strany aplikujeme
a na obe strany aplikujeme  a dostaneme
a dostaneme  - cize mame obe inkluzie a teda aj ziadanu rovnost.
- cize mame obe inkluzie a teda aj ziadanu rovnost.
v druhej implikacii sa mi zda, ze mas pravdu - len to mas napisane trosku nejasne, tak si nie som na 100% isty co tym myslis, tak napisem ja ako som to myslel - ten spor som skonstruoval na trosku inom mieste
Ak  nie je otvorena, tak pre
nie je otvorena, tak pre  plati, ze
plati, ze  -t.j.
-t.j.  . Lenze z (ii) mame
. Lenze z (ii) mame 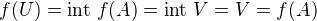 co je spor.
co je spor.
Pozn. Takouto logikou sa to da vlastne dokazat aj priamo - co sa obvykle povazuje za slusnejsi dokaz. Takze by to islo takto:
Vezmime si lubovolnu otvorenu 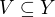 . Oznacme
. Oznacme 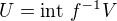 - teda
- teda  je to urcite otvorena. Z (ii) plati
je to urcite otvorena. Z (ii) plati  a teda
a teda 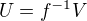 .
.
Offline
