Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 01. 02. 2014 17:10
Re: Lineárna nerovnica
↑ crank139:
Možno previesť na druhú stranu, a dať na spoločný menovateľ 
Netrápte sa nad svojimi problémami s matematikou, môžem vás uistiť, že tie moje sú ešte väčšie. ~~Albert Einstein~~
Jak spozná člověk, že není pitomec ? - Moudrý člověk to nepozná nikdy a blbci je to jedno. ~~Jak přicházejí básnici o iluze~~
Někteří lidi se nikdy nezmění. Anebo se rychle změní a pak se zase rychle změní nazpátek. ~~Homer Simpson~~
Offline
#5 01. 02. 2014 18:46 Příspěvek uživatele Abbysek byl skryt uživatelem Abbysek. Důvod: nepotrebne
#6 01. 02. 2014 18:58 — Editoval Abbysek (01. 02. 2014 19:00)
Re: Lineárna nerovnica

Upravíme do tvaru: 
Vynásobíme -1:  /otocime znak nerovnosti, pretoze nasobime zapornym cislom/
/otocime znak nerovnosti, pretoze nasobime zapornym cislom/
Pomocou diskriminantu vycitame, ze korene z kvadratickej rovnice su -2,73 a 0,7 a korene z menovateľa sú 1 a -1 (pozor, podmienka je, že K sa nesmie rovnať číslu 1 a -1 (otvorené intervaly)
Dáme to spoločne na os:
Výsledkom je interval:
Mýlim sa, tak keď náhodou poradím, pokojne ma opravte.
Offline
#7 01. 02. 2014 21:00
Re: Lineárna nerovnica
a keby som s tej rovnice odobral jednotka, čiže
ako by som to rozlozil? robim to podľa týchto vzorcov no nebol tam uvedený príklad kde sú v menovateli mocniny,
http://www.youtube.com/watch?v=bfh8EUrJSu8
daj si trebars 1:30 tam hneď uvidíš čo mám na mysli, keby tam bolo obyčajné k-1 tak viem čo s celým príkladom ale keď roznásobim ten menovateľ tak nie. dik
Offline
#10 01. 02. 2014 21:35 — Editoval gadgetka (01. 02. 2014 21:35)
Re: Lineárna nerovnica
Jednodušší je to řešit pomocí číselné osy a nulových bodů:
nulové body: 
Naneseš na osu nulové body, dostaneš tak 4 intervaly:
Do nerovnice dosadíš například nulu ( ta leží v druhém intervalu). Celý zlomek ti vyjde záporný. Čili v druhém intervalu se nerovnice chová záporně, v prvním kladně, ve třetím též kladně a ve čtvrtém záporně. Zlomek má být menší než nula, vybíráš tedy ty intervaly, ve kterých máš napsáno mínus.
Řešením je tedy:
Nejsem učitelka, proto matematiku neučím, ale přímo ji řeším...
Offline
#12 01. 02. 2014 21:53
Re: Lineárna nerovnica

Kdy je zlomek menší než nula?
Buď je čitatel menší než nula a jmenovatel větší než nula, nebo naopak, čitatel větší než nula a jmenovatel menší než nula, čili může nastat:
a řešíš:
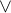

Řešení:
Nejsem učitelka, proto matematiku neučím, ale přímo ji řeším...
Offline
#15 01. 02. 2014 22:15
Re: Lineárna nerovnica
Pravá strana je řešena pomocí nulových bodů nebo ji můžeš zase rozložit stylem: Kdy je součin větší než nula?
Buď 
A řešíš:
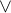

Řešením:
Nejsem učitelka, proto matematiku neučím, ale přímo ji řeším...
Offline
#20 09. 02. 2014 12:25
Re: Lineárna nerovnica

takže podstate nerovnice rozumiem, jediné čo mi vŕta hlavou je že neviem ako a kedy označovať tie nulové body, neviem kedy a kde priraďovaťakú zátvorku v intervale,v krúžku hore je interval otvoreny z oboch strán no do vysledku ho už uzavreli z jednej strany neivem zjakehho dôvodu, pretože keby to nezmenili tak výsledok by bol odpoveď C, vysvetlíte mi niekto ako to je? vďaka vopred
Offline
#21 09. 02. 2014 12:50
- janca361

- .
- Příspěvky: 3284
Re: Lineárna nerovnica
↑ crank139:
No jejich řešení je dost divné. Oni tu jedničku nechtějí dávat do svou intervalů.
Řešením rovnice je interval  , to znamená, že 1 tam patří, 8 ne.
, to znamená, že 1 tam patří, 8 ne.
Přirozená čísla v tomto intervalu: 1, 2, 3, 4, 5, 6, 7 (celkem 7 -> D)
Offline
#22 09. 02. 2014 12:55
- janca361

- .
- Příspěvky: 3284
Re: Lineárna nerovnica
Já bych řešila:

Nulové body: 1 (může nastat) a 8 (nemůže nastat!)
Rozdělím číselnou osu a dosadím vždy jednu hodnotu z intervalu a dostanu znaménka:
----1----(8)---
- + -
Hledám kde je výraz větší než nula, tedy jde je +, proto 
Pak to chce vědět, jak je to s intervaly  -
-  a
a  tam patří,
tam patří,  -
-  a
a  tam nepatří. A co jsou to přirozená čísla (tady není problém, občas, ale může být problém s nulou a zápornými čísly)
tam nepatří. A co jsou to přirozená čísla (tady není problém, občas, ale může být problém s nulou a zápornými čísly)
Offline


 a tu pravu stranu už neviem ako, vidím že to tam máš ale neviem ako si ku tomu prišla keďže sa to už nerieši týmto istým spôsobom ako ľava strana.
a tu pravu stranu už neviem ako, vidím že to tam máš ale neviem ako si ku tomu prišla keďže sa to už nerieši týmto istým spôsobom ako ľava strana.




