Matematické Fórum

Mirgeee · 10. 02. 2014 15:50

Dobrý den!

Nechť A je lineární operátor na Vn, který má n různých vlastních čísel, B je lineární operátor na Vn, který komutuje s A. Mým úkolem je dokázat, že potom je B diagonalizovatelný a každý vl. vektor A je vlastním vektorem B.

Jelikož má A n různých vl. čísel, vl. vektory přísl. těmto číslům tvoří bázi Vn a A je diagonalizovatelný, tedy existuje matice X (z vl. vektorů) a diagonální matice D (vl. čísla na diagonále) tak, že A = X^-1 D X. To, že A a B komutují znamená, že AB = BA. Kdybych dokázal, že A je podobná B, jsem hotov. Myslel jsem, že dál to bude jenom hraní s písmenky, ale nedaří se mi dokázat, že A a B jsou podobné... Můžete mi prosím poradit, jak dál? Díky moc!

Andrejka3 · 10. 02. 2014 19:36

↑ Mirgeee:
Ahoj a co přímo: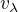
$v_{\lambda}$ vl. vektor A s vl. cislem \lambda. Pak
$X v_{\lambda}=XA(\lambda^{-1}v_{\lambda})=\ldots$

Mirgeee · 10. 02. 2014 21:51

Zdá se mi, že tebou naznačený postup také nikam nevede, nejspíš ho jenom špatně rozvádím. Napadlo mě ještě využít toho, že $(\forall i \in \hat n) BA\vec x_i = AB\vec x_i = \lambda_i B\vec x_i$ , (kde x_i jsou vl. vektory A a zároveň bazické vektory Vn) a prohlásit něco v tom smyslu, že B a A zobrazují bazické vektory na stejnou množinu, takže mají stejné vl. vektory, takže jsou podobné. Prošlo by něco v tom smyslu?

Andrejka3

↑ Mirgeee:
Si mysím, že to je to, co jsem navrhovala. Přímo ukázat, že vlastní vektor A je vlastnim vektorem B. (edit, akorat jsem tam psala X misto B) a ta inverze by se nejak poresila.
$(\forall i \in \hat n) BA\vec x_i = A\color{blue}B\vec x_i \color{black}= \lambda_i \color{blue}B\vec x_i\color{black}$
Jak pises, diky tomu, že spektrum není degenerované, určuje 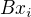$Bx_i$ stejný jednodimenzionální podprostor jako x_i.

Autor skryl část textu. Zobrazit/skrýt!

Matematické Fórum

#1 10. 02. 2014 15:50

Diagonalizace a komutující matice

#2 10. 02. 2014 19:36

Re: Diagonalizace a komutující matice

#3 10. 02. 2014 21:51

Re: Diagonalizace a komutující matice

#4 10. 02. 2014 22:01 — Editoval Andrejka3 (10. 02. 2014 22:09)

Re: Diagonalizace a komutující matice

Zápatí