Matematické Fórum

xdobia09 · 09. 03. 2014 10:49

Dobrý den,
mám příklad:
Nejmenší perioda funkce 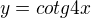$y=cotg 4x$ je
Výsledek: 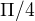$\Pi /4$

Jak vypadá funkce cotg vím, jedna perioda funkce cotg x je pí ... tz. asi chápu jak to ta 4 mění. Ale dokázal by mi to někdo nějak logicky vysvětlit abych do dokázal aplikovat i na další funkce?

Díky za pomoc

Jj · 09. 03. 2014 10:58

↑ xdobia09:

Dobrý den, řešeno zde: Odkaz

xdobia09 · 09. 03. 2014 18:21

Stále nechápu prosím tedy o konkrétní pomoc
První krok:
$Cotg 4x=cotg(4x+p)$

Jenže cotg 0 přece není definován, to už je něco špatně mám takový pocit. Stejně tak nerozumím tomu když Pavel Brožek udělal tento krok 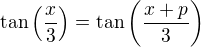$\tan\left(\frac x3\right)=\tan\left(\frac {x+p}3\right)$ . jakto že v čitateli není 3p ... přece po dosazení bych ke zlomku x/3 musel přičíst p/1.

Díky za pomoc