Matematické Fórum

Akcope · 20. 03. 2014 17:27

Zdravím, potřeboval bych pomoc s následujícími dvěmi úlohami:

1) Nalezněte globální extrémy funkce 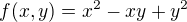$f(x,y) = x^2-xy+y^2$ na množině $M=\{(x,y)\in \mathbb{R}^{2}:|x|+|y|\le 1\}$ .

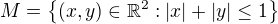Zde nevím, co s Lagrangeovou funkcí. Není diferencovatelná... je třeba rozdělit příklad na 4 případy a počítat každou lagrangeovou funkci zvlášť?

2) Nalezněte globální extrémy funkce 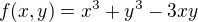$f(x,y) = x^3+y^3 -3xy$ na uzavřeném obdelníku s vrcholy $d_{1}=(0,1),d_{2}=(2,-1),d_{3}=(2,2),d_{4}=(0,2)$ .

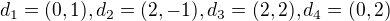Tady mě toho moc nenapadá. Jen spočítat stacionární body bez vazby, zkoumat jak se funkce chová na stranách obdelníka, a popřípadě pak dosadit do jeho vrcholů.

Taky mě napadlo počítat to 4x pro čtyři odlišné vazby (každá pro jednu stranu), které by byly:
x=0
x=2
y=2
y=-1

Ale zde nevím jak funkce "useknout" aby analyticky popisovaly jen tu stěnu obdelníka.

Předem díky za odpověď.

jelena · 20. 03. 2014 23:13

Zdravím,

do tématu patří jen jedna úloha, jinak je diskuse nepřehledná viz pravidla. V obou případech pro vyšetření globálního bych uvažovala lokální extrém na vnitřní oblasti, vyšetření na hranici (1. úloha má hranici), což přejde na vyšetření extrému funkce jedné proměnné + vyšetření na vrcholech.

V úloze 2 mi spíš vyšel lichoběžník (ještě, prosím, zkontroluj souřadnice vrcholů), ale obdobně s 1. úlohou a jak navrhuješ - vyšetřit na přímkách (+vnitřek a vrcholy).

Ale zde nevím jak funkce "useknout" aby analyticky popisovaly jen tu stěnu obdelníka.

to se "usekne", že bod podezřelý z extrému bude mimo oblast vyznačenou vrcholy. Mám dojem, že obdélník stěny nemá.
Pokud nepomůže, tak po jedné úloze do tématu. Děkuji.

Matematické Fórum

#1 20. 03. 2014 17:27

Vázané extrémy funkcí více proměnných

#2 20. 03. 2014 23:13

Re: Vázané extrémy funkcí více proměnných

Zápatí