Matematické Fórum

janca361 · 26. 03. 2014 19:14

Ahoj,
mým úkolem je vést všechny přímky bodem A, které mají s hyperbolou h právě jeden společný bod.
$A[3;1]$
$h:x^{2}-9y^{2}=1$

Dosadila jsme bod A do rovnice hyperboly a zjišťuju, že 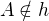$A \notin h$

Autor skryl část textu. Zobrazit/skrýt!

Lze vůbec takové přímky určit?

Díky.

gadgetka · 26. 03. 2014 19:48

Ahoj, ale ten bod A neleží na hyperbole, čili ho nemůžeš do rovnice hyperboly dosazovat, tím bodem jen vede přímka, která má s hyperbolou jeden společný bod, čili tečna hyperboly.

janca361 · 26. 03. 2014 19:52

↑ gadgetka:
Dosadila jsem ho pro ověření, zda je to právě bod dotyku, pak by bylo jednoduché ho dosadit do rovnice tečny (po úpravě hyperboly na středový tvar).

gadgetka · 26. 03. 2014 20:07

Aha, to je jasné. Ještě platí, že většinou tečny, které mají jeden společný bod s hyperbolou, jsou rovnoběžné s aymptotami. Nešlo by jít tímto směrem?

gadgetka · 26. 03. 2014 20:36

Ještě by šlo:
rovnice tečny má tvar $y=kx+q$
Dosadíme do rovnice hyperboly:
$h:x^{2}-9(kx+q)^{2}=1$
$x^2-9(k^2x^2+2kxq+q^2)=1$
$x^2-9k^2x^2+18kxq+9q^2=1$
$(1-9k^2)x^2+18kqx+9q^2-1=0$

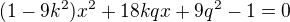
Řešit pro 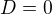$D=0$
a pak do rovnice tečny $y=kx+q$ dosadit bod $A$ , vyjádřit $q$ , dosadí se do výsledku kvadratické rovnice a vyjádří se $k$ .

Jj · 26. 03. 2014 20:43

↑ janca361:

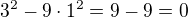Dobrý večer, snad se nepletu, ale řekl bych, že bod A(3,1) leží na asymptotě y = x/3. Takže asi jak uvádí kolegyně ↑ gadgetka: - bodem A vést přímku rovnoběžnou s druhou asymptotou (y=-3), která protne hyperbolu jen v jednom bodě (i když to nebude tečna).