Matematické Fórum

janca361 · 31. 03. 2014 16:19

Ahoj,
asi dělám něco špatně:
Mám řešit pomocí "per partes":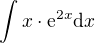
$\int x \cdot \mathrm{e}^{2x} \mathrm{d}x$

$&u=\mathrm{e}^{2x} \text{ } u'=\mathrm{e}^{2x} \cdot \ln \mathrm{e} \cdot 2=2 \cdot \mathrm{e}^{2x}& \\ &v=\frac{x^{2}}{2} \text{ } v'=x&$

$\int x \cdot \mathrm{e}^{2x} \mathrm{d}x=\mathrm{e}^{2x} \cdot \frac{x^{2}}{2} -2\int x \cdot \mathrm{e}^{2x} \mathrm{d}x$
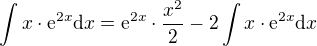
A jsem tam, kde jsem byla.

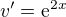Napadlo mě ještě prohodit $u$ a $v'$ , takže $v'=\mathrm{e}^{2x}$ , ale nedokážu se dopracovat k $v$ .

Jak tohle řešit?
Díky.

Takjo · 31. 03. 2014 16:24

↑ janca361:
Dobrý den,
tato cesta vede "do pekla", neboť tímto zvyšujete exponent u x.

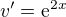Zkuste prohodit $u$ a $v'$ a integrál $v'=\mathrm{e}^{2x}$ řešte pomocí substituce $t=2x$

marnes · 31. 03. 2014 16:25 — Editoval marnes (31. 03. 2014 16:27)

↑ janca361:to je situace, kdy pri integrovani vyjde stejny integral. A to je dobre. Nyni ty dva integraly vpravo dej do leva a mas, ze tri integaly jsou rovny prave strane. Vydel tremi a mas jeden integral

janca361 · 31. 03. 2014 16:31

↑ Takjo:
Ta cesta tam musí být, protože metoda je určena zadání. Jinak jo, nebýt to tam, tak mě asi substituce napadne jako první.

↑ marnes:
Takže takto?
$\int x \cdot \mathrm{e}^{2x} \mathrm{d}x=\mathrm{e}^{2x} \cdot \frac{x^{2}}{2} -2\int x \cdot \mathrm{e}^{2x} \mathrm{d}x \nl 3\int x \cdot \mathrm{e}^{2x} \mathrm{d}x=\mathrm{e}^{2x} \cdot \frac{x^{2}}{2} \nl \int x \cdot \mathrm{e}^{2x} \mathrm{d}x=\frac{\mathrm{e}^{2x} \cdot \frac{x^{2}}{2}}{3}$

Rumburak

↑ janca361:

Ahoj.

Ano, je to špatně. Při Tvém postupu mělo kdyžtak vyjít

$\int x \cdot \mathrm{e}^{2x} \mathrm{d}x= \frac{x^{2}}{2}\cdot \mathrm{e}^{2x} - \int \frac{x^{2}}{2} \cdot 2\mathrm{e}^{2x} \mathrm{d}x$ .

To ale situaci ježtě zhoršilo.

Je třeba klást $u(x) = x , v'(x) = \mathrm{e}^{2x}$ .

janca361 · 31. 03. 2014 16:37

↑ Rumburak:
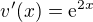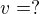Dobře, pokud to řešit takto, tak $v'(x) = \mathrm{e}^{2x}$ a $v=?$ - Netuším, jak se k tomu dopracovat?
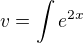$v= \int {e}^{2x}$ ? Ale jak to zintegrovat?

vanok · 31. 03. 2014 16:38

Poznamka:
Ina metoda.
Ak nahodou vies, ze (x.exp(x)- exp(x))'=x.exp(x), tak aj to sa da vyuzit na tvoj vypocet.

marnes · 31. 03. 2014 16:39

↑ janca361:
omluva, nekontroloval jsem cely vypocet, jen reagoval na vznikly problem, ktery muze nekdy nastat, tudiz se muze v budoucnu hodit

Rumburak

↑ janca361: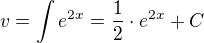

$v= \int {e}^{2x} = \frac{1}{2}\cdot{e}^{2x} + C$ ,

důkaz zpětným zderivováním, případně substitucí $2x = t$ (viz věta o substituci).

Takjo · 31. 03. 2014 16:41

↑ janca361:
Dobrý den,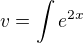
$v= \int {e}^{2x}$ řešte pomocí substituce, viz příspěvek č. 2. ... :)

janca361 · 31. 03. 2014 16:41

↑ marnes:
Snad bude. I tak díky.

Matematické Fórum

#1 31. 03. 2014 16:19

Integrál "per partes"

#2 31. 03. 2014 16:24

Re: Integrál "per partes"

#3 31. 03. 2014 16:25 — Editoval marnes (31. 03. 2014 16:27)

Re: Integrál "per partes"

#4 31. 03. 2014 16:31

Re: Integrál "per partes"

#5 31. 03. 2014 16:32 — Editoval Rumburak (31. 03. 2014 16:37)

Re: Integrál "per partes"

#6 31. 03. 2014 16:37

Re: Integrál "per partes"

#7 31. 03. 2014 16:38

Re: Integrál "per partes"

#8 31. 03. 2014 16:39

Re: Integrál "per partes"

#9 31. 03. 2014 16:41 — Editoval Rumburak (31. 03. 2014 16:42)

Re: Integrál "per partes"

#10 31. 03. 2014 16:41

Re: Integrál "per partes"

#11 31. 03. 2014 16:41

Re: Integrál "per partes"

Zápatí