Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 04. 04. 2014 11:59
goniometrické funkce, rovnice
Ahoj, chci se zeptat, jak je to s g.funkcemi..sin a cos má vždy dvě řešení a tg a cotg má jen jedno a počítá se jen do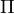 
?? a tedy k sin a co se přičítá vždy 2k 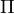a k tg a cotg jen k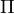? děkuji za všechny reakce...
Offline
- (téma jako vyřešené označil(a) Booback)
#2 04. 04. 2014 12:47
- marnes
- Příspěvky: 11227
Re: goniometrické funkce, rovnice
↑ Booback:
Ano. Pokud v zadání není třeba uvedeno v jakém intervalu, tak ve většině případů jsou u fce sin a cos 2 řešení s periodou 2k(pí) a u tg a cotg 1 řešení s periodou k(pí)
U funkce sin a cos jsou ale "výjimky"
sin x = 1 nebo sin x = -1 je jen jedno řešení v základním intervalu
sin x = 0 je jedno řešení s periodou k(pí)
podobně u fce cos
Jo. A na začátku vás zdravím.
Offline
#3 04. 04. 2014 12:56 — Editoval Honzc (04. 04. 2014 12:58)
Re: goniometrické funkce, rovnice
↑ Booback:
Podívej se na grafy funkcí třeba Sem a pak si uvědom:
1.goniometrické fce jsou funkce periodické (to je platí f(x)=f(x+T), kde T je perioda)
2.sinus a kosinus jsou v těch grafech zakresleny pouze pro jednu periodu. Dále by se už graf zase opakoval. To zn., že perioda těchto funkcí je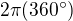 
. To k=...,-2,-1,0,1,2,... udává ve které periodě chceš počítat.
Proč, jak píšeš, jsou hodnotydvě je také vidět z toho grafu. Když si představíš v tom grafu rovnoběžku s osou x (třeba v y=0.5), tak vidíš že ti tato přímka protne graf funkce (v intervalu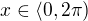 
)dvakrát
Vyjímky viz. ↑ marnes:
3. pro tanges a kotangens je perioda pouze 
a rovnoběžka s osou x protne graf v daném intervalu pouze jednou
Offline