Matematické Fórum

check_drummer · 18. 04. 2014 22:31

Ahoj,
nechť jev J má pravděpodobnost p a ptáme se jaká je střední hodnota s toho, kdy při opakování pokusu poprvé nastane jev J (tedy při kolikátém pokusu průměrně nastane jev J). Pokusy jsou nezávislé. Např. házíme-li kostkou a jev J je, že padne šsetka, pak je p:=1/6 a lze očekávat, že s bude s=1/p=6 - tedy že v průměru padne šestka každých šest pokusů.
Úlohu lze zřejmě řešit výpočtem (není zcela triviální - je nutné najít součet řady $\sum_{i}{x^i.i}$ ). Otázka zní, zda existuje snazší zdůvodnění - ovšem korektní a nikoli pouze intuitivní.

SO(4) · 22. 04. 2014 22:37

Ahoj check_drummer,
v předpisu pro střední hodnotu jsou dvě chyby. Ta první je jednodušší - změnit $x$ na $p$ . Pak máš počítat pravděpodobnost, že J nastane poprvé v $i$ -tém pokusu (v předchozích pokusech J nenastane) a ta je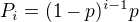
$P_i = (1-p)^{i-1}p$ .
Při výpočtu střední hodnoty se dá postupovat analogicky, jako když se odvozuje střední hodnota Poissonova rozdělení. Opravdu vyjde s=1/p.

check_drummer · 23. 04. 2014 22:42

↑ SO(4):
Ahoj, ale já nepsal vzorec pro střední hodnotu, nýbrž sumu, z jejíž znalosti velikost zkoumané střední hodnoty plyne vhodným dosazením.

SO(4) · 25. 04. 2014 09:32

To mě mělo napadnout, promiň. Asi vím, kam tím míříš, hledanou střední hodnotu je lehké uhodnout, ale nečekaně obtížné spočítat. Tak to neporadím. Čím víc o tom přemýšlím, tím se mi zdá výsledek méně zřejmý.

vnpg · 12. 05. 2014 14:52

Ahoj,

myslím, že nejjednodušší je použít vzorec $E[X] = \sum_{i=1}^\infty = P(X \geq i)$ , který platí pro každou náhodnou proměnnou X nabývající nezáporných celočíselných hodnot (důkaz viz např. na anglické wikipedii, článek Expected value).

V našem případě 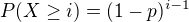$P(X \geq i) = (1 - p)^{i-1}$ , takže uvedený vzorec vyjadřuje E[X] jako geometrickou řadu, jejíž hodnota je 1/p.

Matematické Fórum

#1 18. 04. 2014 22:31

Střední hodnota počtu pokusů, kdy poprvé nastane jev J

#2 22. 04. 2014 22:37

Re: Střední hodnota počtu pokusů, kdy poprvé nastane jev J

#3 23. 04. 2014 22:42

Re: Střední hodnota počtu pokusů, kdy poprvé nastane jev J

#4 25. 04. 2014 09:32

Re: Střední hodnota počtu pokusů, kdy poprvé nastane jev J

#5 12. 05. 2014 14:52

Re: Střední hodnota počtu pokusů, kdy poprvé nastane jev J

Zápatí