Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 16. 03. 2009 21:56 — Editoval O.o (16. 03. 2009 22:15)
Volný pád
Ahoj .-),
jak jsem slíbil, tak jsem tu s novou kapitolou, novým příkladem a novím problémem (pro mne problémem).
Jde znovu o nejjednodušší příklad (nevím, proč končím na nejlehčíš příkladech..) z kapitoly Dynamika hmotného bodu.
Jde o příklad 2/19.
Znou k tomu přiložím strany skript, které jsou věnovány právě takovému typu příkladů.
Tedy skripta dole volný pád.
Dopočítal jsem se k a) nevím, jak to, ale nějak dopočítal, tedy, jak jsem postupoval v části a):
_
y | | |
| T
| | F_G
| \/
|
|
---------------------------------- x
To je můj takový náčrtek situace. Těleso padá dolu, zanedbávám odpor vzduchu, počáteční rychlost (značme v_0) je 0m/s, zrychlení je konstantní.
Dále jsem řešil situaci jen jedním směrem, tedy nepíši vektory, ale vlastně pouze jednu složku (obrázek by byl asi lepší, kdyby šel po ose y, ale to se tady na počítači špatně udělá, tedy na papíře mám osu y identickou s trajektorií pádu).
Vzhledem ke konstantímu zrychlení jsem rovnou vycházel z pohybové funkce: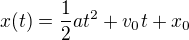 , upravil ji na:
, upravil ji na: 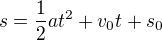 , kde s je dráha a s_0 je počáteční dráha (ta je nulová), tedy:
, kde s je dráha a s_0 je počáteční dráha (ta je nulová), tedy:  (t- čas, a - zrychlení, v_0 - poč. rychlost)
(t- čas, a - zrychlení, v_0 - poč. rychlost)
Na těleso působí pouze jedna síla znázorněná na obrázku označena F_G, kterou nazývám tíhová síla, která je dána vztahem: 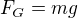 , kde "m" je hmotnost a "g" je tíhové zrychlení - mělo by jít o vektory (stále je neumím v texu zobrazit, prosím pomoc s tímto neduhem jsem z toho nešťastný), ale jak jsem avizoval na začátku, řeším celý příklad jen v jednom směru, tak vektory stejně něpíši.
, kde "m" je hmotnost a "g" je tíhové zrychlení - mělo by jít o vektory (stále je neumím v texu zobrazit, prosím pomoc s tímto neduhem jsem z toho nešťastný), ale jak jsem avizoval na začátku, řeším celý příklad jen v jednom směru, tak vektory stejně něpíši.
Dále vím, že výslednice sil působícíh na těleso je dána součtem všech sil působících na těleso a také vztahem  , kde "m" je hmotnost a "a" je okamžité zrychlení.
, kde "m" je hmotnost a "a" je okamžité zrychlení.
Tedy jen položím rovnost: 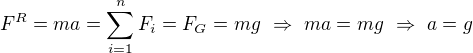 , indexy sil jsem v součtu čísloval, ale vzhledem k tomu, jak jsem označil tíhovou sílu, tak jsem rovnou přepsat.
, indexy sil jsem v součtu čísloval, ale vzhledem k tomu, jak jsem označil tíhovou sílu, tak jsem rovnou přepsat.
Toto bylo důležité do původní rovnice, protože a byla neznámá stejně jako čas a já potřebuji rovnici pro čas, tímto jsem vyřešil, za předpokladu, že g=9,81 (podle dohody, kterou mají asi u nsá na škole možná i jindy co já vím - snad jsem tuto kosntantu nezpletl, nikdy si nejsem jistý tím prvním desetinným místem, tak případně prosím o opravu, děkuji ;-)).
Půjdu rovnou na úpravu rovnice, s kterou jsem začal:
Výsledek mám správně, ale postup musí být špatný. Nerozumím tomu, proč? Konkrétně: ve skriptech je psáno, pokud položím osu y svisle vzhůru, pak platí pro volný pád  , viz. odkaz. Asi jsem někdo něco špatně zvolil a náhodou to vyšlo :-(.
, viz. odkaz. Asi jsem někdo něco špatně zvolil a náhodou to vyšlo :-(.
Část za b) a c) mi nevychází ani přibližně (vlastně jednou mi vyšlo b) téměř (vyšel mi dvojnásobek výsledku, někde se asi dostavila chyba).
Prosím zkušené i nezkušené fyziky/matiky/chemiky/... pomohl by mi někdo?
Předem děkuji..
EDIT: Myslím, že jsem vyřešil moji komplikaci se skripty, řešil jsem v jendom směru, ale v obrázku ho mám vlastně naznačený špatným směrem, ale stále jsem nevyřešil svoji neschopnost vyřešit, tka triviální příklad (přitom mi to připadá jasné).
Moje zamyšlení nad b)
Myslel jsem si, že mohu použít moji původní rovnici jen trochu upravenou, jelikož počáteční rychlost míří opačným směrem a není nulová, změním u ní znaménko, jen mne teď napadlo, jestli je zrychlení stále rovnoměrné, ale kdyby ano, pak moje rovnice bude v cca. takovém to tvaru:  , kde v_0 je 5 m/s a a=g, no co by na to člověk řekl, nevychází to .-).
, kde v_0 je 5 m/s a a=g, no co by na to člověk řekl, nevychází to .-).
Obdobně c) jen rychlost by byla kladná.
Už mi to vychází, neptejte se raději proč, dal jsem do rovnice špatně znaménka, jak jsem si zvolil směr osy y a na začátku ho nedodržoval ;-).
Dokončil jsem to s rovnicemi:
b) 
c) 
PS: Omlouvám se, že jsem s tímhle rušil...
PPS: Teď když tu na to koukám, tak i u triviálního příkladu se strašně rozepíši, ale to jen kvůli vám, abyste to po mne nějak dokázali přelouskat, jinak by to mohlo dopadnout hrůzostrašně (mohl bych to zkrátit a nikdo by nevěděl o co jde, protože v tom dělám strašný chaos ;)).
EDIT II:
Vracím se znovu ke kolizi se skripty:
Vyjdu ze směru podle obrázku, tedy by mi měla vyjít rovnice:  pro zadání b), ale takhle se k výsledku nedá dostat, jsem znovu v koncích a znovu prosím o radu k tomuto příkladu, nejspíš jsem to celé špatně pochopil..
pro zadání b), ale takhle se k výsledku nedá dostat, jsem znovu v koncích a znovu prosím o radu k tomuto příkladu, nejspíš jsem to celé špatně pochopil..
Offline
#2 16. 03. 2009 22:45
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Volný pád
↑ O.o:
Zdravím :-)
zásadní chyba byla vyhodit s_0.
Používej stejná označení jako v materiálech:
poloha balonu (y) je funkce času. V počátečním okamžiku je y_0 = h (300m)
Můžeme vypočítat y v každém okamžiku po celou dobu padu, nás ovšem zajimá okamžík, kdy balon dopadne na zem - tedy, když:
y=0
Rovnice pro volný pad (zadání b) počáteční rychlosti v_0 směrem nahoru), z počáteční výšky y_0=h do konečné polohy y_1=0: 
zadání c)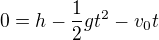
OK?
-----------------------
jak se píše šípka nad vektorem, bylo na LaTex piskovišti.
Offline
#3 16. 03. 2009 23:00
Re: Volný pád
↑ jelena:
Přeji pěkný večer .-),
já už jsem zapomě znovu editovat příspěvek, našel jsem si tom chybu, respk. našel, ale neopravil ji. Počítal jsem něco, co jsem nenakreslil, respk. špatně jsem dosazoval.
Dosatl jsem se k víceméně stejnému závěru jako jsi mi tu napsala ty, což je skvělé (vlastně k identickému zápisu, jen z druhé strany) a jsem ti vděční za vysvětelní ;.).
Slibuji, že se znovu ozvu (určitě zítra =)), tedy nevím, jestli je to zrovna dobrá zpráva, ale zase se rozšíří sekce Fyzika =o)
Ještě jednou ti děkuji a budu doufat v další pomoc a že se budu moci nějak odvděčit.
Offline
#4 18. 03. 2009 21:51
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Volný pád
↑ O.o:
Zdravím :-)
1. k editaci - bylo by velmi vhodne, abys tu editaci vkladal (třeba i barevně) přímo do odstavců, ve kterých došlo k zásadní změně postojů a názorů.
2. Zbytečně si z toho děláš těžkou hlavu (koumáním vzorců) - musíš jen stanovit - co se děje:
pohyb zrychleny s konstantním zrychlením g, "směrem" od zrychlení umíme řešit diferenciální rovnice + odpovídající počáteční podmínky:
-bez počáteční rychlosti, s počáteční rychlosti kladnou, zápornou, s počáteční polohou h.
A kreslí si grafy od zrychlení = f(t) - konstátní přímka, rychlost - přímka se směrnici nenulovou, draha - kus paraboly.
Budu pokračovat v tématu o kruhovém pohybu :-)
Offline