Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 23. 04. 2014 13:51
- cutrongxoay

- Příspěvky: 286
- Pozice: Student
- Reputace: 1
Limita funkce
Zdravim,
opakuji si limity a potreboval bych si ujasnit jejich postup. Nevim jak se na to prislo, z grafu poznam, ale pocetne neumim.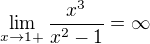
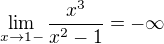
Pomohli byste mi s resenim techto prikladu prosim?
Offline
- (téma jako vyřešené označil(a) cutrongxoay)
#2 23. 04. 2014 14:00
- Crashatorr
- Příspěvky: 360
- Reputace: 7
Re: Limita funkce
↑ cutrongxoay:
Ahoj,
Tyto limity se dají řešit i jednoduchou úvahou. Třeba ta první, počítáš limitu pro x blížící se k 1 zprava. Co dělá čitatel, když se přibližuješ k 1+? Je zhruba jedna, důležitější je jmenovatel. 1 na druhou je jedna -1 je 0, ale ty nedosazuješ přímo jedničku ale pro představu třeba 1,001, takže ten rozdíl ve jmenovateli bude 0,001, a teď si představ že se k té jedničce přiblížíš ještě víc třeba na 1,000001, potom jmenovatel bude 0,000001. A jak se bude chovat celý zlomek? Bude růst, neboť čitatel je stále zhruba jedna a jmenovatel se neustále zvětšuje, tudíž se zvětšuje i hodnota celého zlomku k nekonečnu:)
Offline