Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy z pravděpodobnosti a statistiky
- » Náhodný výběr (TOTO TÉMA JE VYŘEŠENÉ)
#2 25. 04. 2014 09:26
Re: Náhodný výběr
Pokud vybíráme dvojice (x, y) s rovnoměrným rozdělením na ![kopírovat do textarea $[0,1]\times[0,1]$](/mathtex/45/4598fbd50e75f5cbcafa2870323637ad.gif) , tak to je úloha na geometrickou pravděpodobnost. Nakresli si v
, tak to je úloha na geometrickou pravděpodobnost. Nakresli si v 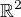 čtverec
čtverec ![kopírovat do textarea $A = [0,1]\times[0,1]$](/mathtex/f6/f68d909218784d5ca0374132fcec52cb.gif) , to odpovídá povolenému rozmezí x a y. Pak si do něj nakresli průnik oblastí
, to odpovídá povolenému rozmezí x a y. Pak si do něj nakresli průnik oblastí
a
a nazvi ho  . To jsou (x, y), které splňují požadovanou vlastnost. Hledanou pravděpodobnost spočítáš jako podíl obsahů oblastí
. To jsou (x, y), které splňují požadovanou vlastnost. Hledanou pravděpodobnost spočítáš jako podíl obsahů oblastí 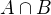 a
a  .
.
Offline
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy z pravděpodobnosti a statistiky
- » Náhodný výběr (TOTO TÉMA JE VYŘEŠENÉ)

 vybereme náhodně dvě čísla, označme je
vybereme náhodně dvě čísla, označme je  a
a  . S jakou pravděpodobností splňují vztah
. S jakou pravděpodobností splňují vztah  ?
?