Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 05. 05. 2014 12:38 — Editoval Freedy (05. 05. 2014 12:41)
Iracionální odmocniny
Ahoj,
před chvílí jsem se tu koukal na téma s odmocninou ze tří. Docela by mě zajímalo, jestli obecně tvrzení, že jakákoliv odmocnina z celého čísla, která není čtvercem jiného přirozeného čísla, musí být iracionální?
Vemu si nějaké nějaké přirozené číslo  kde S je množina čtvercových čísel:
kde S je množina čtvercových čísel: 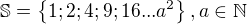
Tak můžu budovat spor na tom, že se odmocnina z A dá zapsat ve tvaru zlomku: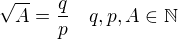 kde q a p jsou nesoudělná čísla.
kde q a p jsou nesoudělná čísla.
Po umocnění dostávám: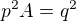
Pokud tedy A není čtvercové číslo, můžu předpokládat že: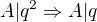
q lze tedy zapsat jako: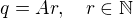 kde q a r jsou nesoudělná čísla.
kde q a r jsou nesoudělná čísla.
Po dosazení do výše uvedené rovnice tedy dostávám: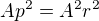
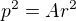 >>> z čehož plyne že:
>>> z čehož plyne že: 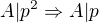
A tedy p a q jsou nesoudelná čísla, přitom mají společného dělitele A.
Lze toto tvrdit, nebo skutečně existuje odmocnina z nečtvercového přirozeného čísla, která je racionální?
Jediné co mě napadlo je tvrdit že: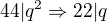 pokud v prvočíselném rozkladu nalezneme alespoň dvě stejná přirozená čísla, tak tento předpoklad, že:
pokud v prvočíselném rozkladu nalezneme alespoň dvě stejná přirozená čísla, tak tento předpoklad, že: 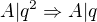 asi nebude platit, nebo spíš nebude přesný.
asi nebude platit, nebo spíš nebude přesný.
L'Hospitalovo pravidlo neexistuje. Byl to výsledek Johanna Bernoulliho
Offline
#2 05. 05. 2014 12:53
Re: Iracionální odmocniny
Pozor, 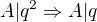 vseobecne neplati.
vseobecne neplati.
Napr. 25|100, ale nie 10.
Tvoj dokaz treba upravit.
Pouzi prvociselny rozklad cisla A.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#3 05. 05. 2014 13:09 — Editoval Freedy (05. 05. 2014 13:17)
Re: Iracionální odmocniny
vanok napsal(a):
Napr. 25|100, ale nie 10.
předpokládám že A není ze čtvercových čísel, ale 25 je 5^2. Samozřejmě to nic neřeší na tom, kdyby tam bylo 50 dělí 100 >> ale 50 už nedělí 10 to chápu.
Prvočíselný rozklad neznámého čísla? Důkaz by teda šel provést obecně na čísla, které lze zapsat ve tvaru: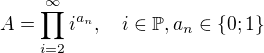
Protože poté by bylo možné předpokládat, že se v prvočíselném rozkladu neobjeví žádná druhá mocnina nějakého přirozeného čísla. Čili například číslo:
2*3*5*7*11*13*17 = 510510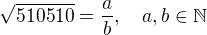
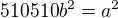
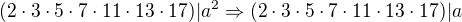
a proto lze zapsat číslo a ve tvaru: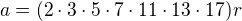 po dosazení:
po dosazení: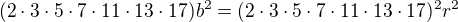
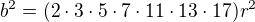
což je hledaný spor.
Ale takto to lze dokázat pouze pro čísla splňující podmínku výše. Jak to lze dokázat pro čísla ve tvaru: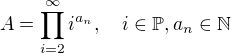 ?
?
Děkuji
Důkaz pro osmičku:
L'Hospitalovo pravidlo neexistuje. Byl to výsledek Johanna Bernoulliho
Offline
#4 05. 05. 2014 13:14 — Editoval vanok (05. 05. 2014 13:21)
Re: Iracionální odmocniny
Ahoj ↑ Freedy:,
Akoze sa to nepohlo, mas nieco nove?
Alebo chces trochu pomoci?
Mame k dispozicii viacej dokazov.
Napisal si 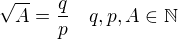 pré nesudelitelne p, q
pré nesudelitelne p, q
(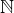 , zda sa ze toto chapes ako nenulove prirodzene cisla, viem ze to zavisi od definicii, ale tak ci tak je to lepsie upresnit )
, zda sa ze toto chapes ako nenulove prirodzene cisla, viem ze to zavisi od definicii, ale tak ci tak je to lepsie upresnit )
Skus dokazat, ze za tvojho predpokladu, mas q=1.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#5 05. 05. 2014 13:34 — Editoval Freedy (05. 05. 2014 14:04)
Re: Iracionální odmocniny
Pokud lze číslo zapsat ve tvaru: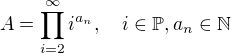
Potom lze předpokládat že: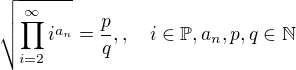
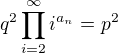
Se součinem jako takovým neumím moc pracovat.
Dle mého názoru pokud tam budou skutečně v prvočíselném rozkladu čtvercová čísla, nebo klidně i vyšší mocniny, lze ten postup zopakovat n způsoby: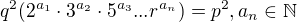
Pokud bych si rozdělil exponenty na sudé a liché můžu psát: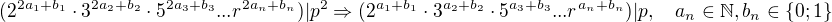
Potom by šlo číslo p vyjádřit ve tvaru: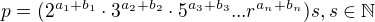
A následně do výše uvedené rovnosti: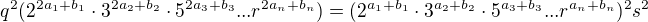
((((((( Bych po vykrácení dostal: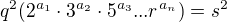 >>> (zde je brutální chyba) )))))))
>>> (zde je brutální chyba) )))))))
""opravím""
Po vykrácení bych dostal: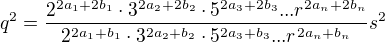
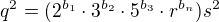
Čili platí: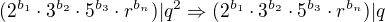 za počátečního předpokladu že
za počátečního předpokladu že 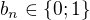
Číslo q nyní lze zapsat ve tvaru: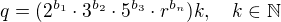
číslo p ale lze zapsat ve tvaru:
Což není nic jiného než: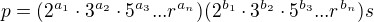
Takže čísla P a Q jsou nesoudělná ale přesto mají společného dělitele: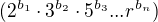
JE TOHLE V POŘÁDKU?
L'Hospitalovo pravidlo neexistuje. Byl to výsledek Johanna Bernoulliho
Offline
#6 05. 05. 2014 13:41
Re: Iracionální odmocniny
vanok napsal(a):
Skus dokazat, ze za tvojho predpokladu, mas q=1.
Pokud jsou p a q nesoudělné a 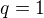 , potom musí být
, potom musí být  . Za tohoto předpokladu je:
. Za tohoto předpokladu je:
Dále ale platí, že pokud je 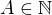 tak:
tak: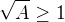
Čili q nemůže být 1.
Pokud teda vycházím z definice: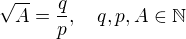 kdy je q čitatel, nikoliv jmenovatel.
kdy je q čitatel, nikoliv jmenovatel.
L'Hospitalovo pravidlo neexistuje. Byl to výsledek Johanna Bernoulliho
Offline
#7 05. 05. 2014 13:45
Re: Iracionální odmocniny
↑ Freedy:,
Mas v tom vyuzitelne myslienky.
O tom ti postupne napisem.
Skus ale najprv ↑ vanok:z tym dokazom, ze q=1.
Je jednoduchy ale treba dobre argumentovat v dokaze. Ak robis mat. Olympiady, moze byt aj tam uzitocny.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#8 05. 05. 2014 13:50
Re: Iracionální odmocniny
V prvním příspěvku jsem psal: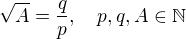
V dalším ale: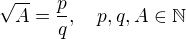
Proto teď nevím, jestli máš na mysli q = 1 jako čitatel nebo jako jmenovatel. Čitatel může být q = 1 pouze za předpokladu, že A = 1 a potom p = 1. Jmenovatel může, ale to pouze za předpkladu že 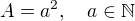
L'Hospitalovo pravidlo neexistuje. Byl to výsledek Johanna Bernoulliho
Offline
#9 05. 05. 2014 13:59 — Editoval vanok (05. 05. 2014 13:59)
Re: Iracionální odmocniny
Myslel som na ten druhy ( to som prehliadol ze tam bola ta inverzia)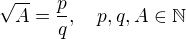 .
.
Umocni to za tvojich predpokladov na druhu,
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#10 05. 05. 2014 14:05 — Editoval Freedy (05. 05. 2014 14:07)
Re: Iracionální odmocniny
V příspěvku 5 jsem editoval řešení, respektive jeho konec. Je to takto v pořádku?
vanok napsal(a):
Myslel som na ten druhy ( to som prehliadol ze tam bola ta inverzia)
.
Umocni to za tvojich predpokladov na druhu,
Ale v případě q = 1 by to potom přeslo do tvaru: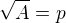 a následně:
a následně: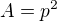
Čili číslo a by bylo druhou mocninou nějakého přirozeného čísla, to znamená, že by dané číslo bylo racionální.
L'Hospitalovo pravidlo neexistuje. Byl to výsledek Johanna Bernoulliho
Offline
#11 05. 05. 2014 14:17 — Editoval vanok (05. 05. 2014 14:23)
Re: Iracionální odmocniny
↑ Freedy:,
Ano, to to dostanes po dokaze, ze q=1,(treba ho urobit)
Predpoklad na zaciatku dokazu je nutne formulovat takto, 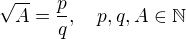 p, q nesudelitelne a zaroven
p, q nesudelitelne a zaroven 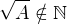 ( co si vlastne predpokladal, v tvojom prvom prispevku , ale tu som ti to zopakoval, aby si to mal n'a mysli)
( co si vlastne predpokladal, v tvojom prvom prispevku , ale tu som ti to zopakoval, aby si to mal n'a mysli)
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#13 05. 05. 2014 14:24
Re: Iracionální odmocniny
Opakujem umocni na druhu 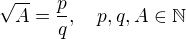 !
!
Napis co to da.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#15 05. 05. 2014 14:42
Re: Iracionální odmocniny
Teraz, napisal si ze  je taky ze p a p su navzajom nesudelitelne.
je taky ze p a p su navzajom nesudelitelne.
Co mozes povedat o 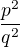 ?
?
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#16 05. 05. 2014 14:59
Re: Iracionální odmocniny
Uvažujme dvě navzájem disjunktní množiny prvočísel: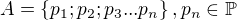
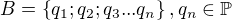
V takovém případě lze zlomek p/q rozložit na součin prvočísel: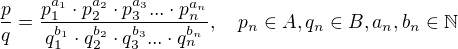
Po umocnění přechází zlomek do tvaru:
Pokud položíme: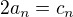
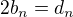
Tak dostáváme: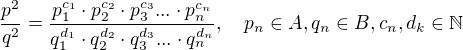
Pokud platí 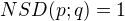 >>> potom platí:
>>> potom platí: 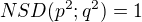
L'Hospitalovo pravidlo neexistuje. Byl to výsledek Johanna Bernoulliho
Offline
#17 05. 05. 2014 15:05 — Editoval vanok (05. 05. 2014 15:09)
Re: Iracionální odmocniny
Pokracujem to znamena, ze v 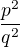
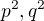 su tiez navzajom nesudelitelne.
su tiez navzajom nesudelitelne.
Akoze  ma jednoznacny prvociselny rozklad,
ma jednoznacny prvociselny rozklad,
rovnost 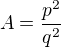 nam okamzite da
nam okamzite da 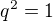 , cize aj
, cize aj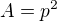 , co je z rozpore z nasim predkladom.
, co je z rozpore z nasim predkladom.
Tym je dokazane, ze....
Poznamka, teraz mozes napisat tento ( zaujimavy) dokaz v jednom prispevku, aby to mohli vyuzit, aj tvoji menej nadani kolegovia.
Otazka, chces pokracovat aj na inych moznych dokazoch?
A tiez ukazat ci nieco podobne neplati aj pre ine odmocniny?
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#18 05. 05. 2014 15:15
Re: Iracionální odmocniny
Já pravdu neznám, o to je to horší, že možná dokazuju něco, co ani dokázat nemůžu, protože to není pravda.
Chci jen vědět, jestli odmocnina z jakéhokoliv přirozeného čísla, které není druhou mocninou jiného přirozeného čísla, je číslo iracionální.
Chápu to správně, že ty mi celou dobu chceš říct, že nemůžu dokazovat něco pro 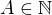 když pro
když pro 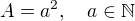 to očividně neplatí?
to očividně neplatí?
Nejde to tedy dokázat obecně?
L'Hospitalovo pravidlo neexistuje. Byl to výsledek Johanna Bernoulliho
Offline
#19 05. 05. 2014 15:24 — Editoval vanok (05. 05. 2014 15:29)
Re: Iracionální odmocniny
Vsak to mas teraz dokazane pre druhu odmocninu.
To je priklad dokazu sporom.
Iny priklad dokazu sporom je aj ten pre druhu odmocninu cisla 2.
Preto je uzitocne, pre teba, napisat do jednej spravny cely dokaz.
Su aj ine dokazy.
Tu ↑ Freedy: pises o akej odmocnine?
Napr pre tretiu odmocninu plati tiez podobna vlasnost....atd.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#20 05. 05. 2014 15:26
Re: Iracionální odmocniny
Takže důkaz v příspěvku 5 je správný?
Samozřejmě se momentálně zabývám druhou odmocninou. Proč se teda řeší, zda-li je odmocnina z 2 nebo 3 iracionální, když můžeme v klidu říct, že odmocnina z jekéhokoliv nečtvercového čísla je iracionální?
L'Hospitalovo pravidlo neexistuje. Byl to výsledek Johanna Bernoulliho
Offline
#21 05. 05. 2014 15:39
Re: Iracionální odmocniny
↑ Freedy:,
Vsak dokaz, co je urobeny plati. Preco pises ak dokazeme ked uz mas jeden dokaz.
V tvojom #5, mas jednu myslienku, ale treba ist dalej. Treba tvoje cislo A rozlozit na 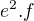 kde f sa neda delit ziadnou druhou mocninou. ( je free-square)... Mozes na tom pracovat...
kde f sa neda delit ziadnou druhou mocninou. ( je free-square)... Mozes na tom pracovat...
Ked napises podrobne ten dokaz, co si ti navrhol, potom by som ti skor ukazal, jeden zalozeny na inom principe... No ak chces. ( ale nie dnes)
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#22 05. 05. 2014 16:08
Re: Iracionální odmocniny
Určitě mám zájem o to vidět i jiný důkaz.
V mém postupu jsou chyby jak tak koukám zpětně. Zkusím ho dotáhnout do konce a taky ho sem přiložit.
L'Hospitalovo pravidlo neexistuje. Byl to výsledek Johanna Bernoulliho
Offline
#23 05. 05. 2014 16:18
Re: Iracionální odmocniny
↑ Freedy:?
To je dobry pristup, ak to vzladnes. Na chybach sa da vela naucit.
Dokaz, co ti chcem ukazat, pracuje na principe, ze kazda neprazdna podmnozina z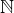 ma najmensi prvok. mozes zacat o tom rozmyslat.
ma najmensi prvok. mozes zacat o tom rozmyslat.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#24 06. 05. 2014 20:00 — Editoval vanok (06. 05. 2014 21:04)
Re: Iracionální odmocniny
Ahoj ↑ Freedy:,
Dnes dam uplne riesenie tvojho vysledku,ktore pouziva ten princip o ktorom som ti vcera na konci pisal. Uvidis, ze je velmi elegantne.
O tomto rieseni len porozmyslaj, ( dobra priprava na vysokolske studia).
Predpokladajme, 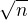 je racionalne, ale nie cele.
je racionalne, ale nie cele.
Uvazujme mnozinu 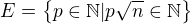 ,
,
tato mnozina je neprazdna. Akoze je podmnozina z 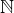 , ma najmensi prvok, oznacme ho
, ma najmensi prvok, oznacme ho 
Potom ![kopírovat do textarea $m(\sqrt n -[\sqrt n])\sqrt n=mn - m \sqrt n [\sqrt n]\in \mathbb{N}$](/mathtex/db/db9ee84a2fca665acab0c4bc6ed1dfe5.gif)
No vsak mame ![kopírovat do textarea $m(\sqrt n -[\sqrt n])=m \sqrt n - m [\sqrt n] \in \mathbb{N}$](/mathtex/6f/6fec6a20fabda70615f7792c4f732af3.gif) , co znamena
, co znamena ![kopírovat do textarea $m(\sqrt n -[\sqrt n]) \in E$](/mathtex/9c/9cb62eb2d365685fe97238299d5fe40b.gif) ale to protireci, minimalite m, pretoze
ale to protireci, minimalite m, pretoze![kopírovat do textarea $\sqrt n -[\sqrt n]<1$](/mathtex/37/37ef1919b71d8bc03c870eb2df3a9358.gif) .
.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#25 07. 05. 2014 10:36
Re: Iracionální odmocniny
Takovéto řešení je sice pěkné, ale moje znalosti ještě bohužel nejsou na takové úrovni. Kdyby jsi měl zájem a vysvětlil mi to podrobně krok po kroku, byl bych ti vděčný. Něco v tom vidím ale vůbec netuším ty přechody. Díky
L'Hospitalovo pravidlo neexistuje. Byl to výsledek Johanna Bernoulliho
Offline

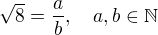 kde a,b jsou nesoudělná čísla
kde a,b jsou nesoudělná čísla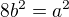
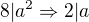
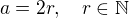
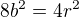
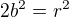


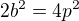
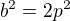 >>>
>>> 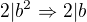 a i b jsou nesoudělná čísla, přesto mají dělitele dvojku.
a i b jsou nesoudělná čísla, přesto mají dělitele dvojku. 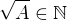 protože
protože