Matematické Fórum

Ospli · 18. 05. 2014 12:38

Poradíte mi, prosím, s následujícími řadami?

$\sum_{n=2}^{\infty }\frac{sin n}{n+10 sin n}$
$\sum_{n=2}^{\infty }\frac{(-1)^{n}}{\sqrt{n}+(-1)^{n}}$

Řekl bych, že obě konvergují a použije se u nich podobný fígl, ale nevím co s nimi.
Když chci použít Dirichletovo kritérium, je tam problém, protože posloupnosti jdoucí k nule nejsou monotónní.
Také řady absolutně divergují srovnáním s harmonickou řadou..
Díky

vnpg · 18. 05. 2014 16:51

↑ Ospli:

Zdravím,

možná že u té první řady by šlo použít následující verzi Abelova kritéria:

"Mějme posloupnosti $(a_n)$ a $(b_n)$ a označme $B_n = \sum_{k=0}^n b_k$ . Předpokládejme, že jsou splněny následující podmínky:

1) Posloupnost 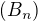$(B_n)$ je omezená; 2) $\sum_{k=0}^\infty | a_{k+1} - a_k | < \infty$ ; 3) $\lim_{k \to \infty} a_k = 0$ .

Potom $\sum_{k=0}^\infty a_k b_k$ konverguje."

Návod na důkaz tohoto kritéria je zde: http://en.wikipedia.org/wiki/Summation_ … plications

V našem případě položme $b_n = \sin n$ a $a_n = \frac{1}{n + 10 \sin n}$ . Potom podmínky 1) a 3) jsou splněny (máme $|B_n| \leq \frac{1}{\sin(1/2)}$ pro všechna $n$ ). Ještě je potřeba ověřit, že platí 2). Myslím, že by to mělo jít.

Ospli · 18. 05. 2014 17:30

Jé to je supr, dík :) U té první řady to vskutku funguje.

U druhé ale řada diferencí z druhé podmínky divergure (je to přibližně harmonická řada) :-/

vnpg · 19. 05. 2014 14:32

U té druhé řady mi vyšlo, že diverguje, konkrétně $\lim_{N \to \infty} \sum_{n=2}^N \frac{(-1)^n}{\sqrt{n} + (-1)^n} = -\infty$ .

Ukazuje to následující úprava: $\frac{(-1)^n}{\sqrt{n} + (-1)^n} = \frac{(-1)^n}{\sqrt{n} + (-1)^n} \frac{\sqrt{n} + (-1)^{n+1}}{\sqrt{n} + (-1)^{n+1}} = \frac{(-1)^n \sqrt{n} - 1}{n-1} = \frac{(-1)^n \sqrt{n}}{n-1} - \frac{1}{n-1}$ .

Ospli · 19. 05. 2014 18:13

↑ vnpg: Děkuju za pomoc.

Matematické Fórum

#1 18. 05. 2014 12:38

konvergence řady

#2 18. 05. 2014 16:51

Re: konvergence řady

#3 18. 05. 2014 17:30

Re: konvergence řady

#4 19. 05. 2014 14:32

Re: konvergence řady

#5 19. 05. 2014 18:13

Re: konvergence řady

Zápatí