Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 25. 05. 2014 16:44 — Editoval Spectrik (25. 05. 2014 16:47)
Úprava výrazu
Ahoj,
mám před státnicema, zbývá mi poslední zkouška na kterou mám již bohužel poslední pokus a když to nedám tak mě vyrazí (předmět opakuju) tak docela sranda. No ale k otázce:
mám výraz:
a potřeboval bych ho upravit na tvar: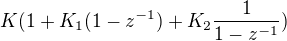
už nad tím sedím docela dlouho a nevím si rady.
Poznámka: Problematika z diskrétního řízení (regulátory)
Offline
#2 25. 05. 2014 17:38
Re: Úprava výrazu
↑ Spectrik: Ahoj, a toto by nepomohlo?
http://www.wolframalpha.com/input/?i=si … F%281-a%29
a držím palce!
Offline
#5 25. 05. 2014 23:41
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Úprava výrazu
↑ Spectrik:
Zdravím,
pokud přeznačím 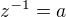 , je potom
, je potom 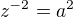 ? Nebylo by jednodušší přidat odkaz na některý materiál, kde je označení? Zde je odkaz na přehled metod, kterou máš v plánu použit? Děkuji.
? Nebylo by jednodušší přidat odkaz na některý materiál, kde je označení? Zde je odkaz na přehled metod, kterou máš v plánu použit? Děkuji.
Offline
#7 26. 05. 2014 09:27
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Úprava výrazu
↑ Spectrik:
potom potřebuješ jen takovou úpravu 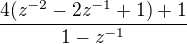 . V pořádku? Děkuji.
. V pořádku? Děkuji.
Offline
#9 26. 05. 2014 11:10
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Úprava výrazu
↑ Spectrik:
můžeš tento výraz 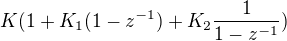 dat ke společnému jmenovateli a porovnat koeficienty u stejných mocnin z (řešení soustavy rovnic) s čitatelem
dat ke společnému jmenovateli a porovnat koeficienty u stejných mocnin z (řešení soustavy rovnic) s čitatelem 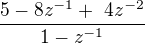 (ale tipuji, že to řešení mít nebude). Zkus sestavit soustavu a vložit do WA.
(ale tipuji, že to řešení mít nebude). Zkus sestavit soustavu a vložit do WA.
Pokud je to řešení diferenční rovnice pomocí zpětné Z-transformace, nestalo by se podívat na původní rovnici? Kontroloval jsi výsledek ve WA? Děkuji.
Offline

 se má najít požadovaný tvar? Pokud pro všechna reálná (nebo komplexní)
se má najít požadovaný tvar? Pokud pro všechna reálná (nebo komplexní)  , tak mi vychází, že úloha nemá řešení. Lze to ověřit např. s použitím substituce
, tak mi vychází, že úloha nemá řešení. Lze to ověřit např. s použitím substituce 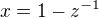 .
.