Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#3 31. 05. 2014 14:14
#5 31. 05. 2014 20:22 — Editoval vnpg (01. 06. 2014 10:09)
Re: Najst jednotkovy vektor
↑ zeus12:
Ahoj,
výsledek u=-2 není správně, protože u je vektor o dvou složkách: 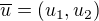 .
.
Protože  je jednotkový vektor, platí
je jednotkový vektor, platí
(1) 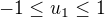 a
a 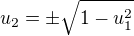 .
.
Naším cílem je najít 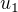 a
a  tak, aby splňovaly (1) a navíc (jak již napověděl ↑ Rumburak:)
tak, aby splňovaly (1) a navíc (jak již napověděl ↑ Rumburak:)
(2) 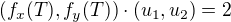 ,
,
kde  je skalární součin, tj.
je skalární součin, tj. 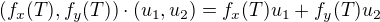 .
.
A pozor na to, že 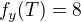 , nikoliv
, nikoliv 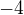 .
.
Offline
#7 02. 06. 2014 09:56 — Editoval Rumburak (05. 06. 2014 09:37)
Re: Najst jednotkovy vektor
↑ zeus12:.
Máš dvě neznámé  , takže potřebuješ soustavu dvou rovnic.
, takže potřebuješ soustavu dvou rovnic.
První rovnici 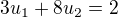 plynoucí z podmínky na směrovou derivaci už máš.
plynoucí z podmínky na směrovou derivaci už máš.
Ještě jsi nepoužil podmínku na "jednotkovost" vektoru 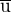 .
.
Co to znamená, že vektor  je jednotkový ?
je jednotkový ?
Offline
#8 02. 06. 2014 13:03
Re: Najst jednotkovy vektor
↑ Rumburak:
Ďakujem veľmi pekne. takže 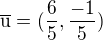 ,teda jednotkovz vektor je 5?
,teda jednotkovz vektor je 5?
Offline
#9 02. 06. 2014 13:16
Re: Najst jednotkovy vektor
↑ zeus12:
Co znamená, že "jednotkový vektor je 5"?
Tvůj vektor 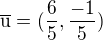 sice splňuje rovnici
sice splňuje rovnici 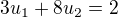 ,
,
ale ne už rovnici 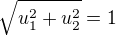 .
.
Prostě vyřeš tuto soustavu rovnic.
Druhou umocníš, aby ses zbavil odmocniny, a dosadíš do ní z první rovnice - dostaneš kvadratickou
rovnici o jedné neznámé, atd. (Jde o látku střední školy.)
Offline
#13 03. 06. 2014 11:56
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Najst jednotkovy vektor
Zdravím,
co je s toho ten jednkotkovy? ta 73??
pokud vektor jste označili 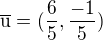 , potom tento zápis
, potom tento zápis
není zápisem jednotkového vektoru, ale jeho normy a tomu má odpovídat označení místo 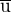 . Tak?
. Tak?
kolega Cheop napsal(a):
Ten jednotkový je celý ten výraz pod odmocnonou, protože to vyjde 1
podle mne celý výraz pod odmocninou není "ten jednotkový" - tak?
kolega Rumburak napsal(a):
Co to znamená, že vektor
je jednotkový ?
No co, konečně? Děkuji
Offline
#15 04. 06. 2014 20:48
#16 05. 06. 2014 09:40
Re: Najst jednotkovy vektor
↑ zeus12:
Co musí splňovat hledaný vektor, aby byl jednotkový, jsem podal zde ↑ Rumburak:
ve skryté nápovědě.
Zdravím kolegyni Jelenu.
Offline

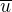 , v smere ktoreho je derivacia funkcie
, v smere ktoreho je derivacia funkcie 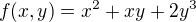 v bode
v bode 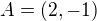 rovna dvom.
rovna dvom.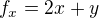 a
a 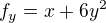 dosadil som si body
dosadil som si body 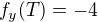
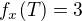
 má v bodě
má v bodě  spojité parciální dericace a tudíž i totální diferenciál,
spojité parciální dericace a tudíž i totální diferenciál,  .
. 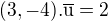
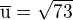 ??
??