Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 31. 05. 2014 17:37 — Editoval blbounNejapny (31. 05. 2014 17:40)
- blbounNejapny

- Zelenáč
- Příspěvky: 17
- Pozice: student
- Reputace: 0
Lineární závislost/nezávislost vektorů
Vyšetřete lineární závislost či nezávislost těchto vektorů z vektorového prostoru polynomů stupně  2
2
F1(x)= x^2 + 2x + 1
F2(x)= x + 1
F3(x)= 1
nemám tušení co s tím mám dělat. Myslím si že se na tom nedá už nic řešit protože trojúhelníkový tvar tam je. Takže bych je určil jako závislé když není vynulovaný žádný řádek.
Offline
#2 31. 05. 2014 18:21
Re: Lineární závislost/nezávislost vektorů
Dobrý den,
Předpokládám, že jste měl na mysli: "Takže bych je určil jako nezávislé když není vynulovaný žádný řádek." V takovém případě je úvaha správná.
Jinak podle definice jsou vektory 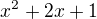 ,
, 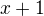 a
a  lineárně nezávislé právě tehdy, když pro všechny skaláry
lineárně nezávislé právě tehdy, když pro všechny skaláry  ,
, 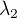 ,
, 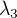 rovnost
rovnost 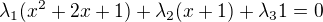 implikuje
implikuje 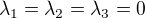 .
.
Offline
#3 31. 05. 2014 20:09 — Editoval kaitlyn (31. 05. 2014 21:07)
Re: Lineární závislost/nezávislost vektorů
↑ blbounNejapny:,
Úlohu můžeš řešit také tak, že polynomy zapíšeš do matice: .
.
Pokud Ti z matice vyjde 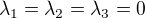 (jak správně uvedl vnpg), pak jsou polynomy lineárně nezávislé! Mrkni ještě na definici LN a bude ti to jasnější :)
(jak správně uvedl vnpg), pak jsou polynomy lineárně nezávislé! Mrkni ještě na definici LN a bude ti to jasnější :)
"Není nám dovoleno vědět vše." (Q. F. Horatius)
"Jediná cesta k vědění je činnost." (G. B. Shaw)
Offline
