Matematické Fórum

madla26 · 31. 05. 2014 19:29

Dobrý den, potřebovala bych poradit s následujícím příkladem:
V osudí je 200 losů, z nichž 10 vyhrává. Jaká je pravděpodobnost, že získáte alespoň jednu výhru, koupíte-li si 20 losů.

Chtěla bych vás především požádat o postup k příkladu.
Moc děkuji za ochotu.

Jj · 31. 05. 2014 20:16 — Editoval Jj (31. 05. 2014 20:17)

↑ madla26:

Dobrý den. Aspoň jeden znamená 1, 2, 3, .... , 9 nebo 10. Zdá se, že lepší to bude přes
doplňkovou pravděpodobnost - spočítat P(žádný los z 20 koupených nevyhrává) a odečíst
ji od jedničky.

Řekl bych, že počet "dvacetic", v nichž není žádný vyhrávající los, se zřejmě bude rovnat $_{200-10 \choose 20}.$

Zbytek už dáte.

madla26 · 01. 06. 2014 08:52

Dobrý den,
takto jsem to právě počítala, ale ve výsledcích mají í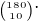 $_{180 \choose 10}.$ jako počet žádných losů, které nevyhrají, jako počet výsledků je uvedeno $_{200 \choose 10}.$
přičemž celé by to mělo být jako 1- (počet žádných losů/počet všech výsledků).

Nerozumím tomu, jak získali ty dvě kombinační čísla.

gadgetka · 01. 06. 2014 09:54

Ahoj, budeš počítat s opačným jevem, že mezi koupenými losy není ani jeden los, co vyhrává:
$1-\frac{{180\choose 10}}{{200\choose 10}}$

madla26 · 01. 06. 2014 10:02

ahoj, to mají i ve výsledkch, ale nechápu, jak vytvořili ty dvě kombinační čísla. Mohla bys mi to prosím rozepsat, jak se na to příjde. Děkuji.

gadgetka · 01. 06. 2014 10:09

Počet všech možných výsledků je ${200 \choose 10}$ , protože v 10 losech z celkových 200 je výhra. Já koupím 20 losů, u kterých předpokládám, že žádná výhra není. Tudíž se mi počet losů, ve kterých je 10 vyhrávajících sníží na 180 a počet příznivých jevů je tak ${180\choose 10}$ .

Jj · 01. 06. 2014 15:24

↑ gadgetka:, ↑ madla26:
Zdravím, já spíš "rozumím" postupu tady ↑ Jj:, tzn. $P = 1 - \frac{{190 \choose 20}}{{200 \choose 20}}=1-\frac{190!\cdot 180!20!}{170!20!\cdot 200!}=$
$=1-\frac{190!\cdot 180!}{170!\cdot 200!}\doteq 0.660$
Ovšem podle postupu kolegyně ↑ gadgetka: to vyjde stejně 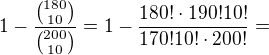$1-\frac{{180\choose 10}}{{200\choose 10}}=1-\frac{180! \cdot 190! 10!}{170! 10! \cdot 200!}=$
$=1-\frac{180! \cdot 190!}{170! \cdot 200!}\doteq 0.660$

takže to bude zřejmě jedno.

Ještě pro doplnění: Řekl bych, že pravděpodobnost získání x vyhrávajících losů ve dvaceti
koupených bude mít hypergeometrické rozdělení (N = 200, m = 10, n = 20), takže
$P(x \ge 1) = 1 - \frac{{10 \choose 0}\cdot {200 -10 \choose 20}}{{200 \choose 20}}= 1 - \frac{1\cdot {190 \choose 20}}{{200 \choose 20}}=\cdots$

maver · 01. 06. 2014 17:30

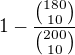
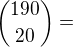${190 \choose 20} =$ ..když vyberu 20 a nic z toho nevyhrává

${200 \choose 20}$ ... všechny možnosti

doplněk do toho je alespoň jeden vyhrává, takže souhlas s Jj

$1 - \frac{1\cdot {190 \choose 20}}{{200 \choose 20}}$

Matematické Fórum

#1 31. 05. 2014 19:29

Pravděpodobnosti jevů

#2 31. 05. 2014 20:16 — Editoval Jj (31. 05. 2014 20:17)

Re: Pravděpodobnosti jevů

#3 01. 06. 2014 08:52

Re: Pravděpodobnosti jevů

#4 01. 06. 2014 09:54

Re: Pravděpodobnosti jevů

#5 01. 06. 2014 10:02

Re: Pravděpodobnosti jevů

#6 01. 06. 2014 10:09

Re: Pravděpodobnosti jevů

#7 01. 06. 2014 15:24

Re: Pravděpodobnosti jevů

#8 01. 06. 2014 17:30

Re: Pravděpodobnosti jevů

Zápatí