Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: pokročilá matematika
- » Rekurentní rovnice (TOTO TÉMA JE VYŘEŠENÉ)
#1 04. 06. 2014 20:35 — Editoval aGr (04. 06. 2014 20:36)
Rekurentní rovnice
Snažím se přijít na řešení rekurentní rovnice 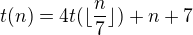 , zadání vyžaduje použití iterační metody.
, zadání vyžaduje použití iterační metody.
Můj postupu vede k  , avšak správné řešení je
, avšak správné řešení je 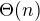 .
.
Ještě poznámka k poslednímu řádku. Došel jsem k  . Protože
. Protože 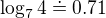 usoudil jsem, že největší z těchto čísel bude
usoudil jsem, že největší z těchto čísel bude 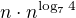 a ostatní členy jsem zanedbal.
a ostatní členy jsem zanedbal.
Předem díky za radu.
Offline
- (téma jako vyřešené označil(a) aGr)
#2 05. 06. 2014 10:02 — Editoval vnpg (05. 06. 2014 10:19)
Re: Rekurentní rovnice
Zdravím,
myslím, že je chyba v té druhé (a tím pádem i třetí) rovnosti. Mělo by být 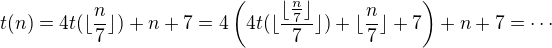 .
.
Jeden způsob řešení mě napadá, akorát si nejsem jistý, zda se pro něj dá použít označení „iterační metoda“. Jde o to, že napíšeme 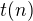 jako teleskopickou řadu
jako teleskopickou řadu 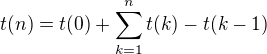 . Diference
. Diference 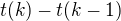 vycházejí poměrně pěkně, protože závisejí jen na hodnotě
vycházejí poměrně pěkně, protože závisejí jen na hodnotě 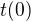 a na tom, jaká je nejvyšší mocnina 7 dělící číslo
a na tom, jaká je nejvyšší mocnina 7 dělící číslo  a zda existují i jiní dělitelé čísla
a zda existují i jiní dělitelé čísla  než 7.
než 7.
Offline
#4 05. 06. 2014 11:26 — Editoval Bati (05. 06. 2014 13:30)
Re: Rekurentní rovnice
↑ Rumburak:↑ vnpg:
Ahoj,
postup ↑ aGr: je dle mého názoru správně až na drobné nepřesnosti jako, že místo 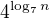 by tam mělo být
by tam mělo být 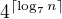 , nebo rovnou psát
, nebo rovnou psát  místo
místo  . Každopádně platí
. Každopádně platí  ,
, 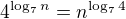 je také ok, geom. řada ok...vyšlo mi to prostě stejně, tedy
je také ok, geom. řada ok...vyšlo mi to prostě stejně, tedy  . EDIT: Přehlédl jsem podstatnou věc, viz příspěvek níže.
. EDIT: Přehlédl jsem podstatnou věc, viz příspěvek níže.
Tím něříkám, že by se to nedalo řešit přehledněji nebo že by se to nedalo převést na klasickou diferenční rovnici (zavedením jiné vhodné posloupnosti).
EDIT: Nejsnáze asi zavedením  , vyřešením (
, vyřešením (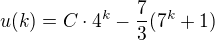 ) a vrácením se k původní proměnné , tj.
) a vrácením se k původní proměnné , tj.  .
.
Offline
#5 05. 06. 2014 13:17
Re: Rekurentní rovnice
↑ Bati:
Ahoj,
díky za upozornění, že  . Z nějakého důvodu jsem předpokládal, že je to špatně, což ve skutečnosti není. Pořád ale v řešení od ↑ aGr: vidím problém v tom, že
. Z nějakého důvodu jsem předpokládal, že je to špatně, což ve skutečnosti není. Pořád ale v řešení od ↑ aGr: vidím problém v tom, že 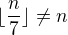 pro
pro  . Pokud někde nedělám chybu, tak mi vychází
. Pokud někde nedělám chybu, tak mi vychází 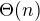 , takže bych tipoval, že záměna
, takže bych tipoval, že záměna 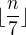 za
za  není korektní.
není korektní.
Ve svém postupu jsem nejprve vypočítal diference. Pro  splňující
splňující 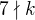 platí
platí 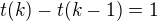 , jak plyne i z příspěvku od ↑ Rumburak:.
, jak plyne i z příspěvku od ↑ Rumburak:.
Nyní uvažujme případ  , kde
, kde 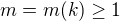 a
a 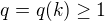 jsou přirozená čísla jednoznačně určená podmínkou
jsou přirozená čísla jednoznačně určená podmínkou 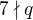 . Potom
. Potom
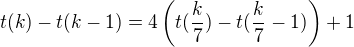 ,
,
odkud indukcí podle  získáme
získáme
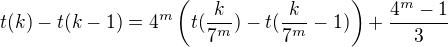 ,
,
a v důsleku toho
 ,
,
kde  je konstanta nezávisící na
je konstanta nezávisící na  . Můžeme vzít např.
. Můžeme vzít např.  .
.
Na základě mezivýsledků o diferencích, které jsme právě odvodili, platí
 ,
,
což napovídá tomu, že výsledek je 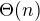 . Je to jen hrubý postup, ale myslím, že by to mělo fungovat. Ještě by to chtělo několik důležitých věcí doplnit. Zejména je třeba ještě dokázat existenci konstanty
. Je to jen hrubý postup, ale myslím, že by to mělo fungovat. Ještě by to chtělo několik důležitých věcí doplnit. Zejména je třeba ještě dokázat existenci konstanty  takové, že
takové, že 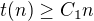 pro všechna dostatečně velká
pro všechna dostatečně velká  .
.
Offline
#6 05. 06. 2014 13:20 — Editoval Brano (05. 06. 2014 13:21)
#9 05. 06. 2014 15:29 — Editoval aGr (05. 06. 2014 15:35)
Re: Rekurentní rovnice
Díky všem za příspěvky. Vidím nyní zásadní chybu v tom, že jsem  nedělil 7 stejně jako jsem to dělal v argumentu. Také se mi líbí trik v postupu od ↑ Brano:, kde zahodil celé části i 7.
nedělil 7 stejně jako jsem to dělal v argumentu. Také se mi líbí trik v postupu od ↑ Brano:, kde zahodil celé části i 7.
↑ Brano: Vím, že bych mohl použít Master Theorem, ale zadání vyžadovalo iterační metodu.
Zde tedy můj opravený postup, doufám si tvrdit, že správný: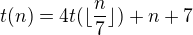
Nyní se nejedná o přesné rovnosti (možná bych měl psát  ), avšak pro zjištění asymtotické složitosti jsou tyhle změny v pořádku.
), avšak pro zjištění asymtotické složitosti jsou tyhle změny v pořádku.
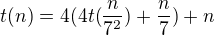
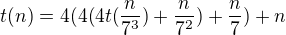
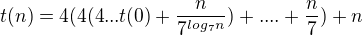
Předpokládejme, že t(0) = 1.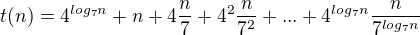

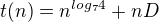
Protože  můžu levou část zanedbat a výsledek je:
můžu levou část zanedbat a výsledek je: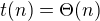
Offline
#10 05. 06. 2014 17:20 — Editoval Brano (05. 06. 2014 17:22)
Re: Rekurentní rovnice
↑ aGr:
btw ak by si chcel to zahodenie konstanty zdovodnit nejak poriadne tak sa to da napr. takto
uvazujme 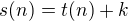 kde
kde  je nejaka fixna konstanta, potom
je nejaka fixna konstanta, potom a teda
a teda 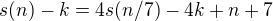 teda
teda 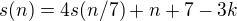 cize ak zvolime
cize ak zvolime  tak konstantny clen vypadne a potom vyjde
tak konstantny clen vypadne a potom vyjde 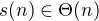 a teda aj
a teda aj  .
.
a len taka poznamocka - trochu viac na mieste je podla mna pisat 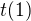 ale da sa obhajit aj zmysluplnost
ale da sa obhajit aj zmysluplnost 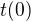 tak pouzivaj to co ste mali na prednaske.
tak pouzivaj to co ste mali na prednaske.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: pokročilá matematika
- » Rekurentní rovnice (TOTO TÉMA JE VYŘEŠENÉ)

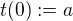 .
. 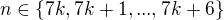 je
je  ,
,  ,
,  t.j.
t.j.  tak potom
tak potom  .
. za
za