Matematické Fórum

jurdastyle · 08. 06. 2014 14:50

Dobry den, prosim vas pomohl by mi nekdo s timto prikladem..

//forum.matweb.cz/upload3/img/2014-06/31557_jarda.png

Udelala bych to takhle:

EX = 0*0,51 + 1*0,35 + 2*0,10 + 3*0,04
EX^2 = 0^2*0,51 + 1^2*0,35 + 2^2*0,10 + 3^2*0,04
VAR X = EX^2 - (EX)^2
o = var x^1/2

nevim jestli jsem to udelala spravne a dale jak v zadani na a) 718 golů, b) 742 golů ?

prosim pomoc :(

Jj · 08. 06. 2014 16:28 — Editoval Jj (08. 06. 2014 16:29)

↑ jurdastyle:

Dobrý den. Řekl bych, že Vaše výpočty jsou zcela správné.

S výpočtem počtu dalších zápasů si nejsem jistý. Možná vyjít z toho že počet zápasů dosud by měl být 696/Ex a odhadnout počet nátných zápasů z průměrného počtu gólů na zápas ( (718-696)/Ex, (742-696)/Ex ).
Ale bylo by lepší, kdyby se k tomu ještě někdo vyjádřil.

jurdastyle · 08. 06. 2014 18:21

↑ Jj:

dekuji ted uz jenom pockat aby nam nekdo potvrdil teorii :)

vnpg · 09. 06. 2014 00:12 — Editoval vnpg (09. 06. 2014 01:12)

↑ jurdastyle: ↑ Jj:
Dobrý den,

myslím, že je správně, co tu bylo napsáno - výpočty od jurdastyle i aproximace od Jj.

Řekl bych, že úloha by se dala formálně zapsat následujícím způsobem:

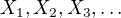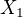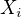Uvažujme náhodné proměnné $X_1, X_2, X_3, \dots$ , kde $X_1$ je počet gólů J. Jágra v nejbližším zápase, $X_2$ je počet gólů J. Jágra v druhém nejbližším zápase atd. Potom můžeme předpokládat, že náhodné proměnné $X_i$ jsou vzájemně nezávislé a mají stejné rozdělení jako náhodná proměnná $X$ v zadání úlohy.

Dále definujeme pro každé 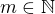$m \in \mathbb{N}$ náhodnou proměnnou $T_m$ předpisem $T_m = \min \{ k \in \mathbb{N} \;\middle| \; \sum_{i=1}^k X_i \geq m \}$ . Takže $T_m$ je pořadí zápasu, ve kterém J. Jágr vstřelí svůj $m$ tý gól, přičemž góly i zápasy počítáme od nuly počínaje přítomností. Chceme spočítat $\mathbb{E}[T_{718-696}] = \mathbb{E}[T_{24}]$ a $\mathbb{E}[T_{742-696}] = \mathbb{E}[T_{46}]$ .

Nyní by to chtělo najít vzorec pro $\mathbb{E}[T_m]$ . To se mi bohužel nepodařilo, ale s použitím rovnosti $\mathbb{P}(T_m \geq k) = \mathbb{P}(X_1 + \cdots + X_{k-1} < m)$ lze odvodit vztah

(1) $\mathbb{E}[T_m] = \frac{1 + 0{,}35 \mathbb{E}[T_{m-1}] + 0{,}1 \mathbb{E}[T_{m-2}] + 0{,}04 \mathbb{E} [T_{m-3}] }{0{,}49}$ ,

který platí pro všechna 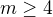$m \geq 4$ . Pokud navíc položíme 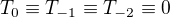$T_0 \equiv T_{-1} \equiv T_{-2} \equiv 0$ , tak lze dokázat, že (1) platí pro všechna $m \geq 1$ .

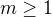Dál se mi to zjednodušit nepodařilo.

Ale např. s pomocí tabulky v Excelu můžeme použít vztah (1) k výpočtu $\mathbb{E}[T_m]$ pro prvních několik tisíc hodnot $m$ . Vychází pak mimo jiné $\mathbb{E}[T_{24}] \approx 36{,}3109824$ a $\mathbb{E}[T_{42}] \approx 63{,}17665404$ .

S použitím aproximace, kterou navrhuje Jj, vychází $\mathbb{E}[T_{24}] \approx 35{,}82089552$ a $\mathbb{E}[T_{42}] \approx 62{,}68656716$ , takže výsledky se shodují po zaokrouhlení na celá čísla.

Je možné, že existuje nějaký elegantní způsob, jak najít vzorec pro $\mathbb{E}[T_m]$ . Ale bohužel nemám tušení, jak jej odvodit.