Matematické Fórum

Simon P40 · 09. 06. 2014 18:36

Extrémy funkce $f(x,y)=x^2+2y^2$ v kruhu $x^2+y^2\le 1$

Jak na to? Já bych to uměl, kdyby nebyl kruh ale $x^2+y^2 = 1$

To dělám tak, že zderivuju funkci a vazební podmínku, dosadím derivace do matice, zjistím diskriminant a položím ho =0.
Z toho vyjádřím proměnnou x a y, které dosadím do vazební podmínky a tím zjistím extrémy.
Ale u toho kruhu nevím jak, díky.

Jozef3 · 09. 06. 2014 19:33

↑ Simon P40:
Jednoduchá rada je, abyste rozdělil na 2 případy, a sice jednotkový otevřený kruh a jeho hranici (na které najít extrémy umíte, jak píšete). Naleznete tedy extrém jednak v otevřeném kruhu, jednak na jeho hranici a tyto extrémy spolu porovnáte, čímž zjistíte extrémy na uzavřeném kruhu.
Na otevřeném kruhu jsou podezřelé z extrému pouze ty body, kde je gradient roven nulovému vektoru. Tedy v tomto příkladě není vůbec složité je najít.

Pokud máte alespoň trochu nadhled, můžete řešení Vašeho příkladu uhádnout (neměl by to být problém, výsledek je opravdu vidět) a pak se rigorózním postupem přesvědčit, že řešení je takové, jak bylo vidět.

Simon P40 · 09. 06. 2014 19:38

Vidím, že se ty body budou pohybovat okolo 0 a 1, ale na správné řešení nadhled nemám ;)
A jak najdu extrémy na otevřeném kruhu? Předpokládám, že otevřený kruh je $x^2+y^2<1$ (?)
Díky moc

Jozef3 · 09. 06. 2014 19:51

↑ Simon P40:
To už jsem Vám vlastně prozradil. Podezřelé body z extrémů na otevřeném kruhu jsou pouze ty, ve kterých je gradient funkce f nulový vektor.

Simon P40

Aha, takže pokud dobře chápu

$\nabla f(x_0,y_0) = (\frac{\partial f(x_0,y_0)}{\partial x},\frac{\partial f(x_0,y_0)}{\partial y})$
$\nabla f(x_0,y_0) = (2x,4y)$ - to je gradient
Nulový vektor bude když x=0 a y=0, že ( $[0,0]$ )?

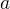Pak mám tedy extrémy u té hranice kruhu $[1,0]$ a $[-1,0],$ [0,1] $a$ [0,-1]$