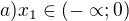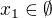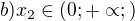Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 29. 03. 2009 14:53 — Editoval Olin (29. 03. 2009 14:54)
Re: Exponenciální funkce
Ten tvůj postup je nějaký strašně komplikovaný, v zásadě možná správný… Ještě by to tam ale chtělo nějak zmínit, co když x = 0.
což je ekvivalentní s
A jsme hotovi.
Offline
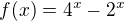 nabývá kladných hodnot.
nabývá kladných hodnot.