Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 24. 06. 2014 15:10
- Blackflower


- Místo: Bratislava
- Příspěvky: 1303
- Škola: FMFI UK BA, EFM, absolvent 2016
- Pozice: aktuár
- Reputace: 71
Ľahký integrál
Ahojte,
toto by som ako tretiačka asi mala vedieť, ale akosi nič...
Zadanie: 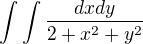 - integruje sa na celom
- integruje sa na celom 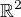
Myslím, že by sa to malo prehodiť do polárnych súradníc, teda: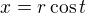
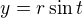
Tak dostanem integrál 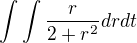 , to sa dá prípadne prepísať na
, to sa dá prípadne prepísať na 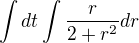 , ale neviem určiť medze. Vedel by mi niekto pomôcť?
, ale neviem určiť medze. Vedel by mi niekto pomôcť?
Prípadne ak by niekomu napadol lepší postup, budem rada.
Offline
- (téma jako vyřešené označil(a) jelena)
#3 24. 06. 2014 16:06
- Blackflower


- Místo: Bratislava
- Příspěvky: 1303
- Škola: FMFI UK BA, EFM, absolvent 2016
- Pozice: aktuár
- Reputace: 71
Re: Ľahký integrál
↑ Hanis: Asi áno... a myslíš, že by mohol byť výsledok nekonečno? Vychádza mi to takto: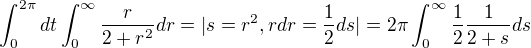
Offline
#4 24. 06. 2014 21:42
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Ľahký integrál
Zdravím,
↑ Blackflower:
pokud jsem nic nepřehlédla, tak můžeš použit i substituci 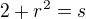 , ale to je jen drobný detail. Spíš ve výsledku bych nenapsala, že integrál je nekonečno, ale že integrál (vnitřní po ds počítaný jako nevlastní) diverguje. Jako vidíš? A odborný kolega ↑ Hanis:? Děkuji.
, ale to je jen drobný detail. Spíš ve výsledku bych nenapsala, že integrál je nekonečno, ale že integrál (vnitřní po ds počítaný jako nevlastní) diverguje. Jako vidíš? A odborný kolega ↑ Hanis:? Děkuji.
Offline
#5 24. 06. 2014 21:45
- Blackflower


- Místo: Bratislava
- Příspěvky: 1303
- Škola: FMFI UK BA, EFM, absolvent 2016
- Pozice: aktuár
- Reputace: 71
Re: Ľahký integrál
↑ jelena: Čiže teoreticky by som mohla počítať niečo ako 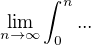 ? Táto limita by teda vyšla nekonečno (ak si dobre pamätám, takto nejako znie veta o tom, kedy integrál konverguje/diverguje).
? Táto limita by teda vyšla nekonečno (ak si dobre pamätám, takto nejako znie veta o tom, kedy integrál konverguje/diverguje).
Offline
#6 24. 06. 2014 21:50
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Ľahký integrál
↑ Blackflower:
no řekla bych, že to jinak ani "počítat" nejde, než s použitím limity (a k nekonečnu se závěrem, že diverguje), jak jsi napsala. Tak, jak jsi uvedla v 1. příspěvku, to je originál úlohy a ve které části úloh se vyskytl?
Offline
#7 24. 06. 2014 21:53 — Editoval Blackflower (24. 06. 2014 21:54)
- Blackflower


- Místo: Bratislava
- Příspěvky: 1303
- Škola: FMFI UK BA, EFM, absolvent 2016
- Pozice: aktuár
- Reputace: 71
Re: Ľahký integrál
↑ jelena: Áno, to bolo vlastne celé zadanie - vypočítať integrál 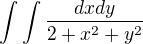 . Nepamätám si úplne presne, ako to bolo zadané, ale určite tam nebolo niečo v zmysle "zistite, či integrál konverguje".
. Nepamätám si úplne presne, ako to bolo zadané, ale určite tam nebolo niečo v zmysle "zistite, či integrál konverguje".
Offline
#8 24. 06. 2014 22:08
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Ľahký integrál
↑ Blackflower:
ano, to je celkem možné, např. ve sbírce Eliaše v kapitole "Nevlastní vicerozměrný integrál" je skupinka úloh
"V úlohách 800 až 807 vypočítejte: 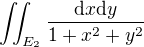 " atd.
" atd.
Tedy počítat jako nevlastní (v tomto případě se závěrem "diverguje").
Offline
#9 24. 06. 2014 22:09
- Blackflower


- Místo: Bratislava
- Příspěvky: 1303
- Škola: FMFI UK BA, EFM, absolvent 2016
- Pozice: aktuár
- Reputace: 71
Re: Ľahký integrál
↑ jelena: Ok, nabudúce budem vedieť :) ďakujem :)
Offline
#10 24. 06. 2014 22:10
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Ľahký integrál
↑ Blackflower:
nemáš za co, raději se ještě podívej i na teorii okolo.
Offline
