Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: pokročilá matematika
- » Magma, homomorfizmus a distibutívne zákony
#1 01. 07. 2014 19:27
Magma, homomorfizmus a distibutívne zákony
Ahoj.
Tak si trochu počítam a neviem či robím niekde chybu, ale je to pri najmenšom zvláštne.
Magmou rozumieme Množinu E spolu s binárnou operáciou. Homomorfizmus medzi magmami je definovaný analogicky ako v teórii grúp.
Zrejme prirodzené čísla spĺňajú definíciu magmy ako pre operáciu sčitovania, tak aj pre operáciu násobenia.
Vezmime si magmu (N,+) a zobrazenie násobenie nasledovne:
Chceme, aby operácia  bola homomorfizmus v prvej a potom aj v druhej premennej;
bola homomorfizmus v prvej a potom aj v druhej premennej; , teda pravý distributívny zákon. Podobne sa urobí ľavý distributívny zákon.
, teda pravý distributívny zákon. Podobne sa urobí ľavý distributívny zákon.
Teraz opačne. Majme magmu  . Požadujme, aby binárna operácia + bola distributívna v prvej premennej.
. Požadujme, aby binárna operácia + bola distributívna v prvej premennej.
Najskôr: 
Požiadavka homomorfizmu:
Tu je tá "zvláštnosť". Očakával som, že to vyjde rovnako. Hoci mám pocit, že tento "vzorec" som už niekde zahliadol ...
Môžete mi k tomu niečo povedať?
Ďakujem.
Offline
#3 09. 07. 2014 19:03
Re: Magma, homomorfizmus a distibutívne zákony
Prirodzené čísla so sčitovaním  tvoria magmu, označme ju
tvoria magmu, označme ju  .
.
Prirodzené čísla s násobením  tvoria magmu, označme ju
tvoria magmu, označme ju  .
.
Uvažujme zobrazenie  definované ako
definované ako  . (binárna operácia)
. (binárna operácia)
Chceme, aby spĺňalo požiadavku homomorfizmu v oboch premenných. Teda: , čo je
, čo je  . Podobne v druhej premennej.
. Podobne v druhej premennej.
Teraz uvažujme zobrazenie  definované ako
definované ako  .
.
Znovu, požiadavka homomorfizmu v oboch premenných: , teda
, teda  .
.
Nech teraz  , teda nech zobrazenie
, teda nech zobrazenie  je zobrazenie
je zobrazenie  . Len prepíšem rovnosť:
. Len prepíšem rovnosť: .
.
Podobne, nech  . Prepíšem rovnosť:
. Prepíšem rovnosť:  .
.
Vyšlo niečo iné, hoci máme rovnaké operácie. Prečo? A posledná rovnosť v prirodzených číslach ani neplatí.
Offline
#4 10. 07. 2014 00:16 — Editoval Andrejka3 (10. 07. 2014 00:25)
Re: Magma, homomorfizmus a distibutívne zákony
↑ :D:
Ahoj.
Nechť  je neprázdná množina,
je neprázdná množina, 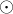 a
a  jsou binární operace na
jsou binární operace na  .
.
Pro libovolné  označme
označme  ,
,  , podobně
, podobně  ,
,
analogicky,  ,
,  ...
...
Požadavek  , to je aby všechny tyhlety fce byly homomorfismy je ekvivalentní
, to je aby všechny tyhlety fce byly homomorfismy je ekvivalentní , tedy že operace
, tedy že operace  je distributivní zleva k operaci
je distributivní zleva k operaci 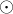 (to není symetrické tvrzení vzhledem k oběma operacím).
(to není symetrické tvrzení vzhledem k oběma operacím).
Analogicky pravá distributivita je ekvivalentní tomu, že  .
.
Zkrátka, nevidím tam problém.
edit: i když, možná jsem to nepochopila, ještě si to projdu.
What does a drowning number theorist say?
'log log log log ...'
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: pokročilá matematika
- » Magma, homomorfizmus a distibutívne zákony
 používáš ve dvou významech, se mi situace jeví jako poněkud nepřehledná.
používáš ve dvou významech, se mi situace jeví jako poněkud nepřehledná.