Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: pokročilá matematika
- » Kvantova mechanika - uplna mnozina spolocnych eigenvektorov
#1 03. 07. 2014 00:14
Kvantova mechanika - uplna mnozina spolocnych eigenvektorov
Zdravim,
nie som si isty, ci su nasledujuce tvrdenia vo vseobecnosti vzdy pravda:
1. Ak sa komutator dvoch operatorov nerovna nule, ich eigenvektory netvoria spolocnu basu (po anglicky to je: complete set of commuting observables - CSCO ). To dava zmysel napriklad pri pauliho maticach ale neviem ci to tak plati pri vsetkych hermitovskych maticach.
2. Ak sa komutator rovna nule, a eigenhodnoty operatorov niesu degenerativne t.z. ze kazda eigenhodnota je ina a zodpoveda jej vzdy iny eigenvektor, ich eigenvektory tvoria vzdy CSCO.
3. Ak sa komutator dvoch operatorov rovna nule a ich eigenhodnoty su degenerativne, ich eigenvektory mozu ale nemusia tvorit CSCO.
p.s. je "complete set of common eigenvektors" to iste ako "complete set of commuting observables" ?
ak ma niekto s tymto viacej skusenosti a vedel by mi pomoct , budem velmi vdacny :)
Offline
#2 15. 07. 2014 22:49 — Editoval Brano (15. 07. 2014 22:50)
Re: Kvantova mechanika - uplna mnozina spolocnych eigenvektorov
Prepokladam, ze chces pracovat iba s konecnymi Hermitovskymi maticami - ak to chces vseobecnejsie tak upresni presne ako.
Ak mas dve Hermitovske matice 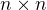 , tak ak existuje nejaka baza
, tak ak existuje nejaka baza  tvorena vlastnymi vektormi aj jednej aj druhej matice, tak ak v nej vyjadris tie matice, potom budu diagonalne a teda nutne musia komutovat.
tvorena vlastnymi vektormi aj jednej aj druhej matice, tak ak v nej vyjadris tie matice, potom budu diagonalne a teda nutne musia komutovat.
Naopak ak komutuju, tak sa da vzdy najst taka baza - treba na to spektralnu vetu a este nejaku drobnu uvahu.
Offline
#3 16. 07. 2014 14:04
Re: Kvantova mechanika - uplna mnozina spolocnych eigenvektorov
↑ zajoxxx:
↑ Brano:↑ Brano:
Pre vsetky konecnedimenzionalne matice (nielen hermitovske) plati: diagonalizovatelne matice A,B komutuju prave vtedy, ked existuje spolocna baza, v ktorej su A,B diagonalne. (Na dokaz spektralnu vetu netreba, da sa to indukciou.)
Podla toho je odpoved na 1. ano - ak nekomutuju, tak spolocnu bazu z eigenvektorov (teda taku, v ktorej su diagonalne) mat nemozu.
"Eigenhodnoty nie su degenerativne" = spektrum je proste, co staci na diagonalizovatelnost, takze urcite nejaku spolocnu bazu z eigenvektorov maju. Akurat eigenvektory nie su urcene jednoznacne (nasobenie skalarom)...
A hermitovske matice su diagonalizovatelne vzdy, takze to iste plati pre degenerativne eigenhodnoty.
Takze by som povedal ze odpoved na 2. je nie a odpoved na 3. ano - vzdy nejaka spolocna baza existuje, ale na to aby sme just dostali musime eigenvektory vyberat nejako rozumne (napr. tak ze eigenvektory budeme normalizovat).
Offline
#4 16. 07. 2014 16:38
Re: Kvantova mechanika - uplna mnozina spolocnych eigenvektorov
↑ Xellos:
a) spektralna veta hovori, ze Hermitovske matice su diagonalizovatelne, teda ak to predpokladas apriori, tak ju samozrejme nepotrebujes :-)
b) preco si myslis, ze na 2. je odpoved nie? Predpokladajme, ze vlastne hodnoty maju vzdy prave jdnorozmerny vlastny priestor (zrejme to sa mysli nedegenerovanostou)
Ak je  vlastny vektor
vlastny vektor  prisluchajuci k
prisluchajuci k  , potom
, potom  cize aj
cize aj  je vlastny vektor prisluchajuci k
je vlastny vektor prisluchajuci k  a teda
a teda  (nedegenerovanost) cize je to vlastny vektor aj matice A - a naopak mame symetricky argument.
(nedegenerovanost) cize je to vlastny vektor aj matice A - a naopak mame symetricky argument.
Takze nech tie vlastne vektory povyberas ako chces, tak to budu vzdy spolocne vlastne vektory nech ich uz normalizujes alebo nie.
c) v bode 3) som to asi pochopil inak ako ty. mne sa zda, ze OP zaujma mozna existencia t.j. vzdy budes vediet taku bazu spolocnych vlastnych vektorov najst; ale samozrejme mas pravdu v tom, ze sa moze stat, ze ak vyberies vlastne vektory jedneho, tak to nemusia byt vlastne vektory druheho.
Trivialny priklad pre nazornost: Nech 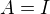 je jednotkova a nech
je jednotkova a nech  je lubovolna Hermitovska. Vsetky vektory su vlastne vektory
je lubovolna Hermitovska. Vsetky vektory su vlastne vektory  - cize by som mohol zobrat lubovolnu bazu
- cize by som mohol zobrat lubovolnu bazu  a je vidiet, ze sa lahko moze stat, ze to nebudu vlastne vektory
a je vidiet, ze sa lahko moze stat, ze to nebudu vlastne vektory  . Na druhu stranu lubovolna baza pozostavajuca z vlastnych vektorov
. Na druhu stranu lubovolna baza pozostavajuca z vlastnych vektorov  je yto co hladame.
je yto co hladame.
Offline
#5 16. 07. 2014 16:55
Re: Kvantova mechanika - uplna mnozina spolocnych eigenvektorov
↑ Brano:
a) Spolocna diagonalizovatelnost je daco ine ako diagonalizovatelnost. Z toho, ze dve matice maju bazy v ktorych su diagonalne, este nevyplyva ze tie bazy mozu byt rovnake.
V bodoch 2. a 3. si nie som isty ako to chapat - mas pravdu ze kazda diagonalna baza jednej matice je aj diag. bazou druhej, ale to neznamena ze neexistuju dve rozne diagonalne bazy. Takze ich eigenvektory mozu tvorit aj dve rozne diagonalne bazy; porovnaj so zadanim "ich eigenvektory tvoria vzdy spolocnu bazu", co ma furt pletie. Neviem ci to ma byt mozna alebo nutna existencia.
Offline
#6 16. 07. 2014 17:16 — Editoval Brano (16. 07. 2014 17:24)
Re: Kvantova mechanika - uplna mnozina spolocnych eigenvektorov
Xellos napsal(a):
↑ Brano:
a) Spolocna diagonalizovatelnost je daco ine ako diagonalizovatelnost. Z toho, ze dve matice maju bazy v ktorych su diagonalne, este nevyplyva ze tie bazy mozu byt rovnake.
samozrejme, a kto tvrdil nieco ine? asi sme sa nepochopili :-)
ja som reagoval na tvoju poznamku, ze na dokaz tvrdenia pre diagonalizovatelne matice nepotrebujes spektralnu vetu. S tym suhlasim, len OP sa pytal na Hermitovske matice takze je potrebne si uvedomit, ze Hermitovske matice su diagonalizovatelne a teda ze odpovedas na to na co sa pytal. Dalej vo svojom prispevku aj samozrejme mas "A hermitovske matice su diagonalizovatelne vzdy" co je presne spektralna veta (resp. jej dosledok - zavisi od formulacie)
a ano zhodneme sa v tom, ze body 2. a 3. su nejasne naformulovane - asi aj preto sa mu na to tak dlho nikto neozyval
PS: najhorsie na tom je to, ze podla mna ani nie je jasne ci OP myslel matice, alebo vseobecne Hermitovske operatory na Hilbertovom priestore. Pre separabilny H. priestor by to snad este mohlo prejst nejak podobne (nie som si uplne isty) ale pre neseparabilny neviem (tam by mohli byt dost problemy s indukciou), ale je dost mozne, ze taky je uz pre QM nezaujimavy.
Offline
#7 16. 07. 2014 19:59
Re: Kvantova mechanika - uplna mnozina spolocnych eigenvektorov
↑ Brano:
Ok, len si to spomenul na divnom mieste - ako keby sa pouzivala pri samotnom dokaze ekvivalencie sucnasnej diagonalizovatelnosti a komutovania, ked je to skor ako overenie predpokladov.
Offline
#8 17. 07. 2014 10:51
Re: Kvantova mechanika - uplna mnozina spolocnych eigenvektorov
Dakujem vam obom za prispevky, v otazke sa jedna iba o operatory v hilbertspace, cize hermitovske matice s realnymi eigenhodnotami atd.
Mne islo v podstate o to, ze ked zadanie znie "zisti ci dva operatory tvoria CSCO" mozeme hned povedat ze NIE iba vtedy, ked nekomutuju. Samotny fakt ze maju degenerativne eigenhodnoty na to nestaci.
V skratke, ak spolu komutuju tak vzdy najdem normalizovane eigenvektory a potom uz viem posudit ci tvoria alebo netvoria spolony set eigenvektorov.
K tej spektralnej vete:
neviem 100% presne (z pohladu linearnej algebry) co to je. My v QM pouzivame spektralny theorem
Offline
#9 17. 07. 2014 12:33 — Editoval Brano (17. 07. 2014 12:38)
Re: Kvantova mechanika - uplna mnozina spolocnych eigenvektorov
Lenze vseobecny Hilbertov priestor nemusi byt konecnorozmerny.
Tu  ti asi chyba este ta vlastna hodnota
ti asi chyba este ta vlastna hodnota
- jedine ze by si mal vlastne vektory normovane tak, ze 
BTW takyto zapis naznacuje, ze vo vseobecnosti uvazujete aj nekonecnorozmerne (dokonca neseparabilne) Hilbrtove priestory, teda uvahy s maticami uplne nestacia.
A este raz; v pripade matic, ak mas komutujuce Hermitovske matice tak vzdy vies najst ON bazu taku, ze obidve v nej budu diagonalne - t.j. bude pozostavat z vlastnych vektorov aj jednej aj druhej matice.
Ak su vsak vlastne hodnoty degenerovane, tak si musis dat trochu pozor ako tu bazu vyberas, ale vzdy sa to da.
Offline
#10 17. 07. 2014 13:45
Re: Kvantova mechanika - uplna mnozina spolocnych eigenvektorov
↑ Brano:
Ano v QM pouzivame vzdy normovane eingenvektory. Ja mam trochu problem so slovenskou terminologiou kedze som toto nikdy nebral po slovensky.
Ako napriklad ci je "spolocna baza" a "kompletny set spolocnych eigenvektorov" to iste.
Napriklad

Pre A mame eigenhodnoty  a eigenvektori
a eigenvektori 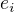



Pre B mame 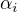 a eigenvektori
a eigenvektori 



V tomto pripade ich eigenvektory ocividne netvoria kompletny set spolocnich eigenvektorov kedze v 3D potrebujem 3 linearne nezavysle vektory. Alebo som tu uplne mimo? Dufam ze som nespravil nikde chybu..
Offline
#11 17. 07. 2014 16:23 — Editoval Brano (17. 07. 2014 16:23)
Re: Kvantova mechanika - uplna mnozina spolocnych eigenvektorov
lenze  u matice
u matice  a tiez
a tiez  u matice
u matice  takze tie vlastne vektory mozes vyberat aj inak.
takze tie vlastne vektory mozes vyberat aj inak.
Len v tomto pripade to mas jednoduche, lebo si to vybral pomerne dobre uz na prvykrat.
Ked zvolis  tak
tak 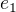 je vlastny vektor
je vlastny vektor  prislichajuci k
prislichajuci k  a tiez je to vlastny vektor
a tiez je to vlastny vektor  prisluchajuci
prisluchajuci  potom
potom  je vlastny vektor
je vlastny vektor  prisluchajuci znova k
prisluchajuci znova k  a tiez je to vlastny vektor
a tiez je to vlastny vektor  prisluchajuci k
prisluchajuci k  a na zaver
a na zaver  je vlastny vektor
je vlastny vektor  prisluchajuci k
prisluchajuci k  a vlastny vektor
a vlastny vektor  prisluchajuci k
prisluchajuci k 
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: pokročilá matematika
- » Kvantova mechanika - uplna mnozina spolocnych eigenvektorov
