Matematické Fórum

check_drummer · 11. 07. 2014 23:15

Ahoj,
četl jsem článek, ve kterém se píše, že máme-li vztažnou soustavu V1 a označíme-li čtveřicí (x,y,z,t) souřadnice bodu [x,y,z] v čase t, pak v takovéto soustavě platí, že 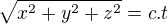$\sqrt{x^2+y^2+z^2}=c.t$ - což popisuje body, do kterých dospěl parsek vyslaný v čase t=0 z počátku. Po úpravě získané rovnosti máme (*) 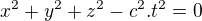$x^2+y^2+z^2-c^2.t^2=0$ , Pokud tutéž úvahu provedeme pro vztažnou soustavu V2, která se vůči V1 pohybuje rovnoměrně přímočaře, tak pro souřadnice (indexuji je indexem 2) bodů v ní obsažené získáme analogicky vztah (**) $x_2^2+y_2^2+z_2^2-c^2.t_2^2=0$ .
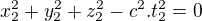Na základě toho prý vyplývá, že je 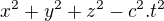$x^2+y^2+z^2-c^2.t^2$ invariantem - tedy že má tento výraz ve V1 a V2 (pro odpovídající souřadnice) stejnou hodnotu. I kdyby byly osy x,y,z,t v obou soustavách rovnoběžné a v čase t=0 splývaly počátky obou soustav, pak mi to tvrzení o invariantu nějak neplyne - to, že se (*) a (**) rovnají 0 přece neznamená, že jsou-li levé strany (*) a (**) rovny jiné hodnotě, že se rovněž rovnají.

Děkuji za objasnění nebo za názory.

Jj · 12. 07. 2014 10:52

↑ check_drummer:

Zdravím, pokud mě paměť nekladme, tak invariantnost výrazu vyplývá ze speciálního principu relativity:
Je-li v soustavě (*) čelem světelné vlny koule, má být v soustavě (**) čelem světelné vlny taky koule.
Z toho pak také plyne, že je nutně 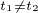$_{t_1 \not= t_2}$ .

Ale paměť je paměť ...

check_drummer · 12. 07. 2014 14:37

↑ Jj:
Ahoj, ono se to týká celé speciální teorie relativity. To, že (*) a (**) popisují kouli je v podsstatě jasné - není mi však jasné, proč jde o invariant.

Brzls · 13. 07. 2014 06:23

Zdravim

Bohuzel ted nemam moc casu a domu se dostany az pristi tyden, ale urcite by stalo za to vzit ten vyraz, a vyjadrit ho v obecne vztazne soustave pomoci Lorentzovi transformace (ktera se odvozuje mezavisle, nejde tedy o zadne dokazovani v kruhu). Pokud se nemylim, po upravach bysme meli dostat ten samy vyraz. To by znamenalo ze ma stejnou hodnotu ve vsech vztaznych soustavach - jde tedy o invariant. Ale mozna se pletu, timhle bych nic mene zacal...

check_drummer · 14. 07. 2014 03:13

↑ Brzls:
Ahoj, děkuji za názor. Ovšem použití Lorenztovy transformace jsem se chtěl vyhnout - naopak jsem ji chtěl odvodit na základě právě uvedeného invariantu.

Brzls · 14. 07. 2014 04:13

↑ check_drummer:

Ahaa tak to nad tim zkusim jeste popremyslet. Ale jak jsem rikal, loretzova transformace se da odvodit i bez tohoto

MirekH · 17. 07. 2014 21:19

↑ check_drummer:
Zdravím,
pokud správně chápu vznesený dotaz, tak jde o to dokázat invarianci časoprostorového intervalu nejen pro světelný případ, ale i pro časupodobný a prostorupodobný. Pokud se omezíme na méně prostorových dimenzí, lze invarianci v obou případech ukázat celkem názorně.

Časupodobný:
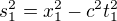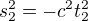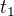Mějme dvě události vzdálené o $s_1^2 = x_1^2 - c^2t_1^2$ v jedné soustavě a o $s_2^2 = -c^2t_2^2$ v druhé soustavě, tj. že se v ní odehrají na stejném místě. Pokud umístíme zrcadlo do takové vzdálenosti $y$ , aby světelný paprsek přeletěl z pozice první události do druhé (s odrazem o zrcadlo) za čas $t_1$ , bude zřejmě platit z Pythagora 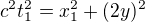$c^2t_1^2 = x_1^2 + (2y)^2$ , tedy 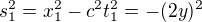$s_1^2 = x_1^2 - c^2t_1^2 = -(2y)^2$ , ale zároveň i 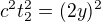$c^2t_2^2 = (2y)^2$ , protože se pohybujeme pouze ve směru $x$ , $y$ se nemění. Potom $s_2^2 = -c^2t_2^2 = -(2y)^2 = s_1^2$ .

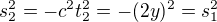Prostorupodobný:
Tady by se ještě více než předtím hodil obrázek, ale když si nakreslíme v časoprostorovém diagramu prostoru podobnou úsečku délky 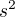$s^2$ a doplníme ji na čtyřúhelník ze světelných paprsků, jehož ona bude diagonálou, tak druhou diagonálou bude časupodobná $-s^2$ . Jelikož se při přechodu do jiné soustavy zachová pravoúhlost a délka časupodobné diagonály, zachová se i délka té prostorupodobné.

Myslím, že je jako fyzikální důkaz je to ok, nějaká matematicky přijatelnější verze by už byla méně názorná, ale myšlenky by byly podobné.

Brzls · 25. 09. 2015 13:22

↑ check_drummer:
Nedávno jsem si vzpomněl na toto téma, sice je pravděpodobné, že už jsi odpověď na tvojí otázku našel, nicméně stejně bych rád ještě do diskuze přispěl, třeba na to v budoucnu někdo narazí.

0. Newtonů zákon (ten o inerciálních soustavách)
1. Množinu všech událostí (tedy čtveřic x,y,z,t) nazveme časoprostorem. Metriku v tomto prostoru zavedeme jako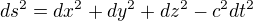
$ds^{2}=dx^{2}+dy^{2}+dz^{2}-c^{2}dt^{2}$ kde c je konstanta zavedená níže.

2. Ve vakuu se světlo šíří rovnoměrně přímočaře konečnou rychlostí c, která je stejná ve všech inerciálních soustavách.

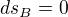Z tohoto předpokladu lehce odvodíme (tak jako v příspěvku 1.) fakt, že pokud v soustavě A $ds_{A}=0$ tak i v soustavě $ds_{B}=0$ (mlčky vynechávám slovo inerciální, ale snad je to jasné)

Pro tyto diferenciály by tedy mělo platit, že 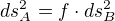$ds_{A}^{2}=f\cdot ds_{B}^{2}$
Kde v tuto chvíli je funkce f obecně $f=f(v,v^{i},x^{j},t)$

3. Funkce f nezávisí na souřadnicích v časoprostoru.

Takovýto postulát je rovnocenný s postulátem o homogenitě časoprostoru. S fyzikální intuice požadujeme aby všechny body byly "ekvivalentní". Nicméně pokud celou teorii budujeme od začátku, tak to můžeme formulovat i takto

4. Funkce f nezávisí na složkách rychlosti.

To samé jako v bodě tři - tentokrát požadujeme izotropii prostoru, žádný směr nesmí být preferován.
Jediné na čem tedy funkce f závisí je velikost rychlosti v.
Závěr:
Platí tedy 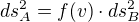$ds_{A}^{2}=f(v)\cdot ds_{B}^{2}$ jenže při přechodu ze soustavy B do A platí ten samý vztah
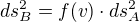$ds_{B}^{2}=f(v)\cdot ds_{A}^{2}$ spojením dostaneme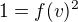
$1=f(v)^{2}$

5. Teď se musí nějak zdůvodnit, proč platí 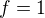$f=1$ (nikoli -1). Myslím, že záporné znaménko by nás později dovedlo do sporu. Další možnost je říci, že uvažujeme pouze lineární transformace (chceme aby se rovnoměrný pohyb opět zobrazil na rovnoměrný při přechodu do jiné soustavy) a z toho už znaménko + vyplývá.

Nevím jestli to lze provést nějak ještě obecněji, ale tohle by měl být taky způsob jak k invarianci dospět, navíc obsahuje poměrně málo "fyziky".

Xellos · 25. 09. 2015 14:03

↑ Brzls:

$ds_{A}^{2}=f\cdot ds_{B}^{2}$
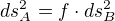
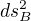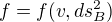Tu predpokladas nejaku linearitu, co vobec nemusis. Lepsie je dat $ds_{B}^{2}$ do argumentu funkcie $f$ . Ked potom dojdes k $f=f(v,ds_{B}^{2})$ , mozes si vsimnut ze nemas k dispozicii nic co by malo rozmer casu a len jedinu vec s rozmerom dlzky - 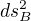$ds_{B}^{2}$ , takze to linearne byt musi aby sedeli rozmery. Konkretne, linearita tvaru

$ds_{A}^{2}=F(v)\cdot ds_{B}^{2}+G(v)$

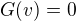a $G(v)=0$ zo spec. pripadu svetlo.

To, ze 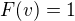$F(v)=1$ , potom odvodime ak zoberieme 3 sustavy a prechody 1->2 a 1->3->2.

Zdroj: http://utf.mff.cuni.cz/~semerak/STR.pdf, cast 3.5.

Brzls · 25. 09. 2015 15:03 — Editoval Brzls (25. 09. 2015 15:06)

↑ Xellos:
Svatá pravda. Svým způsobem mi to přijde triviální, ale je pravda že to stojí za zmínku. Použít tři různé soustavy místo dvou je jistě lepší.

Ještě jsem viděl někde toto. V tom odkaze je řečeno, že F nesmí záležet na přírůstcích souřadnic, ale nepřijde mi to tak triviální. Takže když uvážíme, že lorentzova transformace bude muset být lineární, tak jistě platí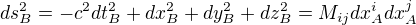
$ds_{B}^{2}=-c^{2}dt_{B}^{2}+dx_{B}^{2}+dy_{B}^{2}+dz_{B}^{2}=M_{ij}dx_{A}^{i}dx_{A}^{j}$

Kde M je nějaká matice, jejíž koeficienty jsou funkce souřadnic a rychlosti, to že nezávisej na souřadnicích plyne z homogenity.
Stejně jako před tim odvodíme, že když je ds=0 tak to platí ve všech soustavách. Využijeme toho, že ten vztah musí platit pro libovolný přírůstky (svázaný podmínkou, že ds=0), a vhodnou volbou (napřed dosadíme dx, potom -dx, dvě ze tří prostorových souřadnic, tedy jejich přírůstků položíme rovno nule atd.) nám z toho taktéž vypadne, že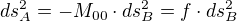

$ds_{A}^{2}=-M_{00}\cdot ds_{B}^{2}=f\cdot ds_{B}^{2}$ navíc už máme zaručeno, že to závisí jen na rychlosti.

Zbytek je stejný

MichalAld

Tohle už je sto let staré, ale kdyby tě to ještě zajímalo...

check_drummer napsal(a):
četl jsem článek, ve kterém se píše, že máme-li vztažnou soustavu V1 a označíme-li čtveřicí (x,y,z,t) souřadnice bodu [x,y,z] v čase t, pak v takovéto soustavě platí, že $\sqrt{x^2+y^2+z^2}=c.t$

Tohle je samo o sobě nesmysl, to obecně neplatí. Platí to právě jen pro ty body, do kterých se dostane záblesk světla, vyslaný z počátku v čase 0.

check_drummer napsal(a):
Pokud tutéž úvahu provedeme pro vztažnou soustavu V2, která se vůči V1 pohybuje rovnoměrně přímočaře, tak pro souřadnice (indexuji je indexem 2) bodů v ní obsažené získáme analogicky vztah (**) $x_2^2+y_2^2+z_2^2-c^2.t_2^2=0$ .
Na základě toho prý vyplývá, že je $x^2+y^2+z^2-c^2.t^2$ invariantem - tedy že má tento výraz ve V1 a V2 (pro odpovídající souřadnice) stejnou hodnotu.

To, že je daný výraz invariantem plyne z toho, že požadujeme aby ta rychlost světla byla v obou soustavách stejná. Že v obou soustavách vytvoří záblesk stejnou "světelnou kouli" a její velikost roste stejnou rychlostí.

Tedy že L/t = c (L je ten výraz pod odmocninou, Pythagorova věta) dá stejnou hodnotu c v obou soustavách (ve všech soustavách)

Já neumím matematicky dokázat, že jediná transformace, která to splňuje je zrovna ta Lorentzova (minimálně to neumím bez explicitního požadavku na linearitu transformace), ale uvádí se, že linearitu lze dokázat, pokud požadujeme aby to platilo ve všech bodech a směrech prostoru stejně. Což je takový celkem přirozený požadavek.

Když už tu transformaci nalezneme, není asi problém ukázat, že vzah je invariant, i když není roven nule.
(ale teď mi dochází, že tys to asi chtěl dokázat přímo, bez odvozování Lorentzovy transformace, tak to já samozřejmě nevím. Snad jen skrze důkaz, že dané číslo je skalár (tenzor nultého řádu)).

Matematické Fórum

#1 11. 07. 2014 23:15

Invariant speciální teorie relativity

#2 12. 07. 2014 10:52

Re: Invariant speciální teorie relativity

#3 12. 07. 2014 14:37

Re: Invariant speciální teorie relativity

#4 13. 07. 2014 06:23

Re: Invariant speciální teorie relativity

#5 14. 07. 2014 03:13

Re: Invariant speciální teorie relativity

#6 14. 07. 2014 04:13

Re: Invariant speciální teorie relativity

#7 17. 07. 2014 21:19

Re: Invariant speciální teorie relativity

#8 25. 09. 2015 13:22

Re: Invariant speciální teorie relativity

#9 25. 09. 2015 14:03

Re: Invariant speciální teorie relativity

#10 25. 09. 2015 15:03 — Editoval Brzls (25. 09. 2015 15:06)

Re: Invariant speciální teorie relativity

#11 11. 03. 2018 15:24 — Editoval MichalAld (11. 03. 2018 15:35)

Re: Invariant speciální teorie relativity

check_drummer napsal(a):

check_drummer napsal(a):

Zápatí