Matematické Fórum

Jencek · 30. 07. 2014 16:20 — Editoval Jencek (30. 07. 2014 16:22)

Ahojte :)

Mohli by jste mi prosím Vás poradit, co s tímto příkladem? Respektive, jak se dostanu přes derivace partikulárního řešení? :)

$y^3 +2y^2 = \frac{2-2x}{x^3}$

Dokážu to rozdělit partikulární řešení

$y= C_{1}+C_{2}x+C_{3}e^{-2x}$

Poté to zapíši jako homogenní rovnici

$y= C"_{1}+C"_{2}x+C"_{3}e^{-2x}$

Tady už nevím jak dál, protože když to zderivuji ještě jednou, tak derivace 1čky u $C"_{1}$ =0 tudíž mi C1 vypadne a nedokážu to vypočítat, možná se mýlím a postup je špatně.

" značí 1. derivaci

Děkuji za odpověď

Eratosthenes · 30. 07. 2014 21:11

ahoj ↑ Jencek:,

předpokládám, že rovnice je

$y''' +2y'' = \frac{2-2x}{x^3}$

jinak by nebyla diferenciální.

$y= C_{1}+C_{2}x+C_{3}e^{-2x}$

není partikulární řešení, ale obecné řešení homogenní rovnice. Teď musíš najít řešení rovnice původní. To hledáš ve tvaru

$Y(x)= C_{1}(x)+C_{2}(x)\cdot x+C_{3}(x)\cdot e^{-2x}$

Takže třikrát zderivovat a dosadit do zadané rovnice...

Xellos · 30. 07. 2014 23:05 — Editoval Xellos (30. 07. 2014 23:22)

↑ Eratosthenes:

Ehm, aj podla nazvu vlakna by bolo lepsie pouzit variaciu konstant, teda najst funkcie $C_{1..3}(x)$ tak aby platilo:

$C_1'(x)+C_2'(x)x+C_3'(x)e^{-2x}=0$
$C_2'(x)-2C_3'(x)e^{-2x}=0$
$4C_3'(x)e^{-2x}=\frac{2-2x}{x^3}$

Kedze fundamentalny system ma konstantnu a linearnu funkciu, tak vyjde sustava rovnic taka jednoducha ze staci integrovat 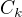$C_k$ od poslednej rovnice a dosadzovat vzdy do predoslej.

$C_3(x)=\int\frac{1-x}{2x^3}e^{2x}\mathrm{d}x=-\frac{1}{4x^2}e^{2x}+c_3$
(postup: per partes na integral $\frac{1}{x^3}e^{2x}$ , po prvom kroku sa vykrati s integralom $\frac{1}{2x^2}e^{2x}$ )

$C_2(x)=\int{\frac{1-x}{x^3}\mathrm{d}x}=-\frac{1}{2x^2}+\frac{1}{x}+c_2$

$C_1(x)=\int{\frac{x-1}{2x^3}-\frac{1-x}{x^2}\mathrm{d}x}=\frac{1}{4x^2}+\frac{1}{2x}+\ln{|x|}+c_1$

Ostava len podosadzovat $C_{1..3}$ do vseobecneho riesenia.

Matematické Fórum

#1 30. 07. 2014 16:20 — Editoval Jencek (30. 07. 2014 16:22)

Variace konstant

#2 30. 07. 2014 21:11

Re: Variace konstant

#3 30. 07. 2014 23:05 — Editoval Xellos (30. 07. 2014 23:22)

Re: Variace konstant