Matematické Fórum

Ahoj ↑ check_drummer:,
Mozno toto ti postaci
http://www.math.cornell.edu/~hatcher/AT/AT.pdf

↑ check_drummer:

Podle mě nejnázornější vysvětlení je skrze singlární homologii topologických prostorů (taktéž v onom Hatcherovi, jak odkazuje ↑ vanok:) - přinejmenším to osvětluje pojmy jako "cykly" a "hranice" (Hatcher k tomu navíc bude mít spoustu obrázků : )) ). Jakmile si tam člověk trochu zvykne na formální sumy singulárních simplexů, dává to docela dobrý názor na to, co se tam děje.

Jinak pro bližší studium nějakých homologických teorií bych doporučil toho Hatchera zkombinovat s nějakým textem zabývajícím se čistě homologickou algebrou (např. J. Rotman - Introduction to homological algebra). Spoustu těch věcí tam Hatcher dělá "na koleni" a je v tom vidět snaha vyhnout se formulacím v řeči kategorií, což mi přijde občas víc na škodu, než k užitku.

↑ check_drummer:

No já nejsem až tak moc na geometrické představy, ale tak zkusit to můžu.

1) Primitivní obrázek toho, jak to vypadá algebraicky (který není z mé hlavy):


Vysvětlení:
Velké elipsy jsou abelovské grupy - jednotlivé "články" řetězcového komplexu (obrázek je zavádějící v tom, že vypadají stejně - nemusí být). Ty červené kužely mezi nimi jsou pak homomorfismy grup - tzv "diferenciály" těch jednotlivých "článků". Křížek v každé grupě je neutrální prvek. Tedy prostřední elipsy jsou jádra diferenciálů a fialové kužely restrikce dif. na jádro (tj zobrazuje jádro na nulu). Vnitřní elipsy jsou obrazy diferenciálů (všimni si: podmínka je totěž, jako že ). Ta modrá věc ukazuje, co to znamená vzít tou homologickou grupu řetězcového komplexu - je to zkrátka něco, co měří interval "od obrazu předchozího k jádru následujícího" diferenciálu (tj. zelenou oblast).

2) (Návod, jak asi získat něco, co lze chápat jako) geometrická intuice  (která už vůbec není moje):
K tomu je podle mě nejlepší uvažovat aplikaci v singulární homologii).

Mějme nějaký topologický prostor , k němuž chceme přiřadit nějaké abelovské grupy, a to nějak tak, aby to něco zajímavého o té topologii vypovídalo.

Tak ho začneme "ostřelovat křivkami" - tj vezmeme jednotkový interval a budeme uvažovat všechna spojitá zobrazení , což je něco, co si můžeme představit jako "orientovanou čáru na prostoru X":



Ta množina všech spoj zobrazení na sobě však bohužel nemá a priori žádnou vhodnou strukturu grupy. Tak abychom ji tam nějak dostali, můžeme zkusit generovat všemi těmito zobrazeními volnou abelovskou grupu. Zní to trochu brute force, ale výhodu to má tu, že se v tom stále ještě dá docela dobře uvažovat geometricky: když budou 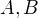dvě takové křivky, pak je něco jako "třikrát jdi po A a pak jednou po B".

(Což je hezký pocit, že to jde, ale je to trochu nepřesné: 1) co je to je poněkud záhadné, protože, to má smysl uvažovat jako "třikrát projdi A pozpátku", ale je to něco jiného než , kde je "skutečně" křivka projitá pozpátku - tj ; 2) podobně matoucí je, že to sčítání je komutativní - tedy  "třikrát jdi po A a pak jednou po B" je tot06, co  "jdi jednou po B a pak třikrát po A".)

Teď: Podobně můžeme postupovat "o dimenzi níž": Tj. místo intervalu vzít bod a uvažovat "spojitá zob. z   do ", což je totéž, jako "zob. z   do ," což je de facto totéž, jako "body X" a necháme jimi volně generovat grupu. Přirozený způsob, jak tyto dvě grupy nějak k sobě vztáhnout, je: křivce A přiřadíme body, které spojuje. Teď se hodí, že máme u koeficientů znaménka - umožní nám to pamatovat si, který z těch dvou bodů je počáteční a který koncový bod křivky A. Tedy definujeme grupový homomorfismus, kter7 je na generátorech předepsán .

Teď co se stane, když vezmeme grupu, generovanou body, modulo obraz tohoto homomorfismu: Jde o to, že pro libovolnou křivku na vlastně prohlašujeme body a za stejné, neboli: Kdykoli body a na umíš spojit křivkou, považuj je za stejné. A skutečně, platí, že takhle definovaná grupa je isomorfní sumě kopií 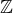, kde za každou křivkově souvislou komponentu dostaneme jednu kopii 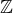. Tedy takto definovaná grupa měří počet křivkově souvislých komponent zkoumaného topologického prostoru.

No a co to má co dělat s řetězcovými komplexy: To, co jsem popsal, je konstrukce prvních dvou článků v singulárním řetězcovém komplexu top. prostoru . Obecně člověk takto "ostřeluje" daný prostor nějakými -rozměrnými simplexy (což je: bod, interval, trojúhelník, plný čtyřstěn, ...) a diferenciály konstruuje tak, že simplexu nějak systematicky přiřazuje sumu jeho stěn, ze kterých se skládá hranice toho simplexu (tj čtyřstěnu sumu jeho stěn, trojúhelníku sumu stran..). Pak má pěknou interpretaci magickým pořekadlem "hranice hranice je prázdná" (fakt, který platí např. v kontextu topologických variet s hranicí), apod. Výsledkem je, že ti homologie tohoto řetězcového komplexu dají šikovné invarianty, které jsou zachovány třeba homeomorfismem (a obecněji homotopickou ekvivalencí). Problém samozřejmě je, jak je nějak prakticky počítat, ale to už je jiná otázka.