Matematické Fórum

jarrro · 17. 08. 2014 20:06 — Editoval jarrro (17. 08. 2014 20:09)

čaute pri čítaní topologickej literatúry ma prekvapilo, že produktová topológia ktorá zachováva veľa dôležitých vlastností pri ľubovoľnej indexovej množine nezachováva v prípade nespočítateľnej indexovej množiny metrizovateľnosť existuje nejaká topológia na produkte zachovávajúca všetko čo zachováva produktová (generovaná vzormi otvorených množín v projekciách) a čo navyše zachováva pri ľubovoľnej kardinalite indexovej množiny metrizovateľnosť, ale má zmysel aj pre nemetrizovateľné priestory a v prípade spočítateľných indexových množín sa zhoduje s produktovou topológiou?

Brano · 18. 08. 2014 00:27

to je dost siroka otazka - lebo topologii si mozes navymyslat kolko chces - problem je nakolko budu prirodzene

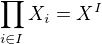existuje vsak jedna velmi prirodzena, ktora ale nefunguje uplne vseobecne. keby si mal situaciu, ze vsetky priestory ktore chces nasobit su tie iste; t.j. $X_i=X$ (povedzme ze metrizovatelny) tak potom vlastne $\prod_{i\in I}X_i=X^I$ t.j. priestor funkcii z $I$ do $X$ . sucinova topologia je vlastne topologia bodovej konvergencie, ktora je pre pripad nespocitatelneho $I$ nemetrizovatelna, ale ina velmi prirodzena topologia - konkretne topologia rovnomernej konvergencie je metrizovatelna

takze inspirovani touto topologiou si mozme skusit zadefinovat pre lubovolny system metrickych priestorov 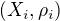$(X_i,\rho_i)$ definovat metriku na 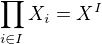$\prod_{i\in I}X_i=X^I$ takto $\rho(\{x_i\},\{y_i\})=\sup_{i\in I}\rho_i(x_i,y_i)$ - len si musis pooverovat ci tam nieco nezlyha

ale v skutocnosti som ti presne na tvoju otazku neodpovedal, lebo aj topologia rovnomernej konvergencie aj to zovseobecnenie je priamo viazane na to, ze tam uz mas metricku strukturu (alebo aspon uniformitu) na jednotlivych "suradnicovych" priestoroch a nedava moznost to definovat vseobecne pre topologicke priestory

ale mozno to trochu pomoze

Brano · 18. 08. 2014 03:11

↑ vanok:
mozno som si tam nieco nevsimol, ale tam bola iba klasicka sucinova metrika pre spocitatelne vela metrickych priestorov + tvrdenie ze v takom pripade generuje topologiu zhodnu so sucinovou topologiou

vanok · 18. 08. 2014 04:32

Ahoj ↑ Brano:,
Mas pravdu. Je to zbytocny prispevok. Skryjem ho.

jarrro · 18. 08. 2014 09:21

↑ Brano:↑ Brano:díky áno myslel som topológiu ktorá sa dá definovať aj v prípade, že ani na jednom priestore nepoznáme (a ani nemusí existovať) metriku ak sa z metrík skonštruuje metrika tak je jasné, že topológia generovaná guľami v tej novej metrike je tiež metrizovateľná je to vlastne definícia metrizovateľnosti
ale suprémová metrika generuje pre nekonečné indexové množiny obecne inú topológiu ako produktová a inú ako boxová čiže suprémová je ostro medzi produktovou a boxovou aspoň tak píše Munkres.

Brano · 18. 08. 2014 15:06 — Editoval Brano (18. 08. 2014 15:58)

↑ jarrro:
a pre nespocitatelne je jasne, ze sa nemozu zhodovat ved to priamo pozadujes, lebo sucinova je nemetrizovatelna a ty chces metrizovatelnost od tej topologie
(a na nekonecnych spocitatelnych ... no hej je to smola :) nejak som prehliadol, ze v spocitatelnych pozadujes zhodu so sucinovou)

no a moj prispevok bol o tom ako dat navod na konstrukciu takej metriky (priamo v tom pripade kde to chces korigovat)

malo to byt skor ako inspiracia ktorym smerom uvazovat - totizto nejaka bezne pouzivana taka nie je a ked si chces nejaku vymysliet, tak niekde treba zacat

jarrro · 18. 08. 2014 16:16

ďakujem myslel som si že to ešte asi známe nebude lebo inak by sa o tom písalo a nepoužívala by sa produktová topológia, ale táto "vylepšená"

Matematické Fórum

#1 17. 08. 2014 20:06 — Editoval jarrro (17. 08. 2014 20:09)

Topológia na produkte zachovávajúca metrizovateľnosť

#2 18. 08. 2014 00:27

Re: Topológia na produkte zachovávajúca metrizovateľnosť

#3 18. 08. 2014 00:40 — Editoval vanok (18. 08. 2014 00:44) Příspěvek uživatele vanok byl skryt uživatelem vanok. Důvod: Zbytocna poznamka

#4 18. 08. 2014 03:11

Re: Topológia na produkte zachovávajúca metrizovateľnosť

#5 18. 08. 2014 04:29 Příspěvek uživatele vanok byl skryt uživatelem vanok. Důvod: Zbytocna poznamka

#6 18. 08. 2014 04:32

Re: Topológia na produkte zachovávajúca metrizovateľnosť

#7 18. 08. 2014 09:21

Re: Topológia na produkte zachovávajúca metrizovateľnosť

#8 18. 08. 2014 15:06 — Editoval Brano (18. 08. 2014 15:58)

Re: Topológia na produkte zachovávajúca metrizovateľnosť

#9 18. 08. 2014 16:16

Re: Topológia na produkte zachovávajúca metrizovateľnosť

Zápatí