Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 27. 09. 2014 10:44
- janca361

- .
- Příspěvky: 3284
Součet aritmetické řady
Zdravím,
nějak se nedokážu dobrat výsledku - úkolem je vyjádřit součet následující aritmetické řady v závislosti na n jako polynomiální funkci.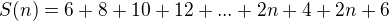
Součet aritmetické řady: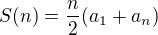
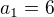
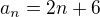
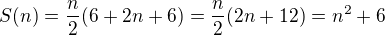
Správný vysledek by měl být 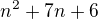
Offline
- (téma jako vyřešené označil(a) janca361)
#2 27. 09. 2014 10:53 — Editoval misaH (27. 09. 2014 10:55)
- misaH
- Příspěvky: 13460
Re: Součet aritmetické řady
↑ janca361:$
Asi máš zle predpis pre n-tých člen, už pre druhý člen to nesedí.
Pravdepodobne zmätky pri číslovaní členov - od 0 alebo od 1.
Offline
#3 27. 09. 2014 11:05
Re: Součet aritmetické řady
Ahoj,
ty uvažuješ, tvým předpisem, že první člen je s indexem 0 a nikoliv 1.
Výsledek totiž vypadá, jako by počítal s indexem 0, protože aby jsi dostala součet prvního členu, musíš bezpodmínečně dosadit 0 za n.
Proto výsledných členů nebude n ale n+1 a dostáváš tedy: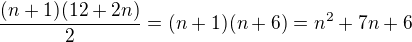
L'Hospitalovo pravidlo neexistuje. Byl to výsledek Johanna Bernoulliho
Offline
#4 27. 09. 2014 11:22 — Editoval misaH (27. 09. 2014 11:26)
#5 27. 09. 2014 11:22
- janca361

- .
- Příspěvky: 3284
Re: Součet aritmetické řady
No nenapadlo mne uvažovat, že jinde mohou číslovat jinak.
Díky.
Offline
